Dual optimization for convex constrained objectives without the gradient-Lipschitz assumption

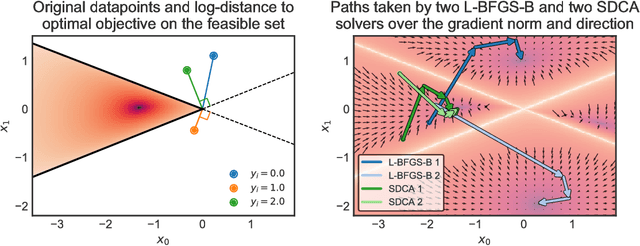
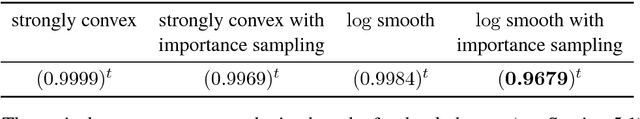
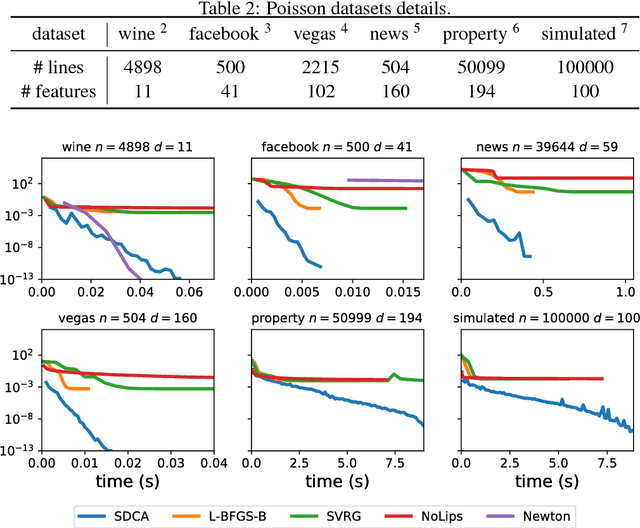
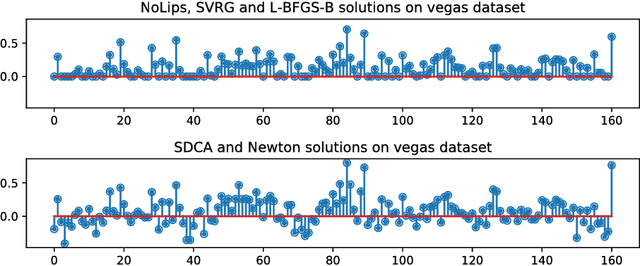
The minimization of convex objectives coming from linear supervised learning problems, such as penalized generalized linear models, can be formulated as finite sums of convex functions. For such problems, a large set of stochastic first-order solvers based on the idea of variance reduction are available and combine both computational efficiency and sound theoretical guarantees (linear convergence rates). Such rates are obtained under both gradient-Lipschitz and strong convexity assumptions. Motivated by learning problems that do not meet the gradient-Lipschitz assumption, such as linear Poisson regression, we work under another smoothness assumption, and obtain a linear convergence rate for a shifted version of Stochastic Dual Coordinate Ascent (SDCA) that improves the current state-of-the-art. Our motivation for considering a solver working on the Fenchel-dual problem comes from the fact that such objectives include many linear constraints, that are easier to deal with in the dual. Our approach and theoretical findings are validated on several datasets, for Poisson regression and another objective coming from the negative log-likelihood of the Hawkes process, which is a family of models which proves extremely useful for the modeling of information propagation in social networks and causality inference.