Double Ramp Loss Based Reject Option Classifier
Paper and Code
Dec 08, 2014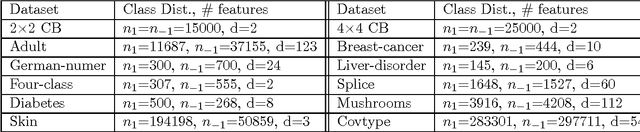
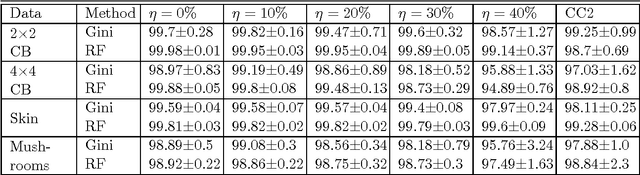
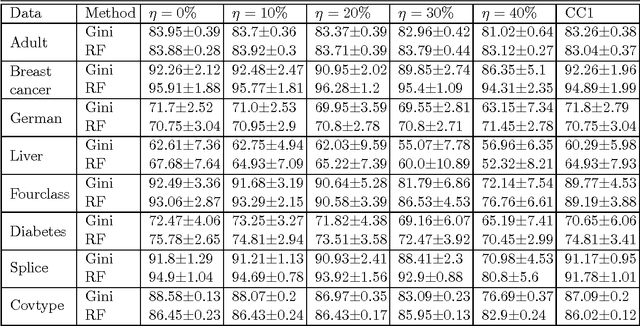
We consider the problem of learning reject option classifiers. The goodness of a reject option classifier is quantified using $0-d-1$ loss function wherein a loss $d \in (0,.5)$ is assigned for rejection. In this paper, we propose {\em double ramp loss} function which gives a continuous upper bound for $(0-d-1)$ loss. Our approach is based on minimizing regularized risk under the double ramp loss using {\em difference of convex (DC) programming}. We show the effectiveness of our approach through experiments on synthetic and benchmark datasets. Our approach performs better than the state of the art reject option classification approaches.
* DBLP:conf/pakdd/2017-1
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge