Do semidefinite relaxations solve sparse PCA up to the information limit?
Paper and Code
Jun 03, 2015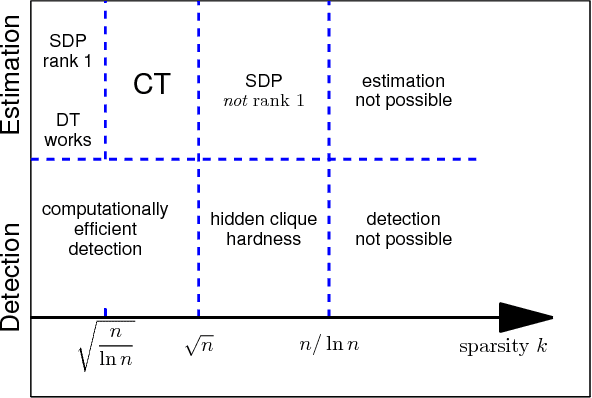
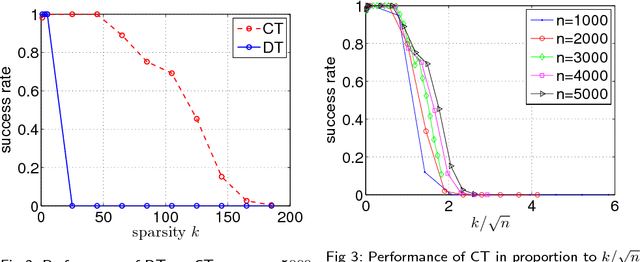
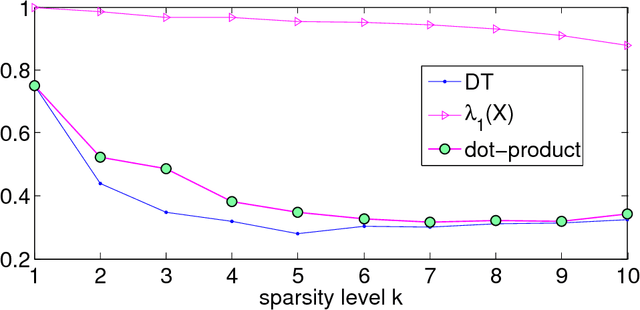
Estimating the leading principal components of data, assuming they are sparse, is a central task in modern high-dimensional statistics. Many algorithms were developed for this sparse PCA problem, from simple diagonal thresholding to sophisticated semidefinite programming (SDP) methods. A key theoretical question is under what conditions can such algorithms recover the sparse principal components? We study this question for a single-spike model with an $\ell_0$-sparse eigenvector, in the asymptotic regime as dimension $p$ and sample size $n$ both tend to infinity. Amini and Wainwright [Ann. Statist. 37 (2009) 2877-2921] proved that for sparsity levels $k\geq\Omega(n/\log p)$, no algorithm, efficient or not, can reliably recover the sparse eigenvector. In contrast, for $k\leq O(\sqrt{n/\log p})$, diagonal thresholding is consistent. It was further conjectured that an SDP approach may close this gap between computational and information limits. We prove that when $k\geq\Omega(\sqrt{n})$, the proposed SDP approach, at least in its standard usage, cannot recover the sparse spike. In fact, we conjecture that in the single-spike model, no computationally-efficient algorithm can recover a spike of $\ell_0$-sparsity $k\geq\Omega(\sqrt{n})$. Finally, we present empirical results suggesting that up to sparsity levels $k=O(\sqrt{n})$, recovery is possible by a simple covariance thresholding algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge