Do Diffusion Models Suffer Error Propagation? Theoretical Analysis and Consistency Regularization
Paper and Code
Aug 09, 2023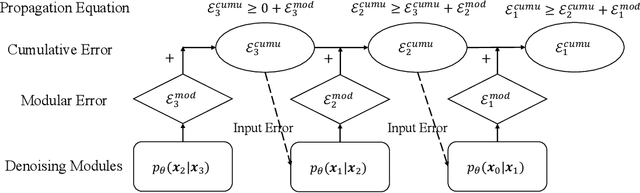

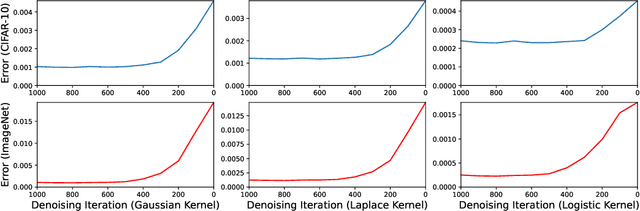

While diffusion models have achieved promising performances in data synthesis, they might suffer error propagation because of their cascade structure, where the distributional mismatch spreads and magnifies through the chain of denoising modules. However, a strict analysis is expected since many sequential models such as Conditional Random Field (CRF) are free from error propagation. In this paper, we empirically and theoretically verify that diffusion models are indeed affected by error propagation and we then propose a regularization to address this problem. Our theoretical analysis reveals that the question can be reduced to whether every denoising module of the diffusion model is fault-tolerant. We derive insightful transition equations, indicating that the module can't recover from input errors and even propagates additional errors to the next module. Our analysis directly leads to a consistency regularization scheme for diffusion models, which explicitly reduces the distribution gap between forward and backward processes. We further introduce a bootstrapping algorithm to reduce the computation cost of the regularizer. Our experimental results on multiple image datasets show that our regularization effectively handles error propagation and significantly improves the performance of vanilla diffusion models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge