DM$^2$: Distributed Multi-Agent Reinforcement Learning for Distribution Matching

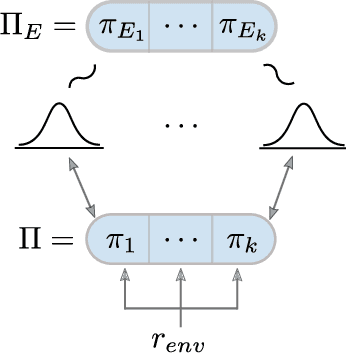
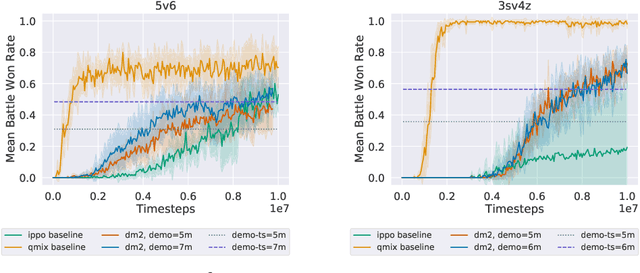
Current approaches to multi-agent cooperation rely heavily on centralized mechanisms or explicit communication protocols to ensure convergence. This paper studies the problem of distributed multi-agent learning without resorting to explicit coordination schemes. The proposed algorithm (DM$^2$) leverages distribution matching to facilitate independent agents' coordination. Each individual agent matches a target distribution of concurrently sampled trajectories from a joint expert policy. The theoretical analysis shows that under some conditions, if each agent optimizes their individual distribution matching objective, the agents increase a lower bound on the objective of matching the joint expert policy, allowing convergence to the joint expert policy. Further, if the distribution matching objective is aligned with a joint task, a combination of environment reward and distribution matching reward leads to the same equilibrium. Experimental validation on the StarCraft domain shows that combining the reward for distribution matching with the environment reward allows agents to outperform a fully distributed baseline. Additional experiments probe the conditions under which expert demonstrations need to be sampled in order to outperform the fully distributed baseline.