Distribution Grid Modeling Using Smart Meter Data
Paper and Code
Feb 28, 2021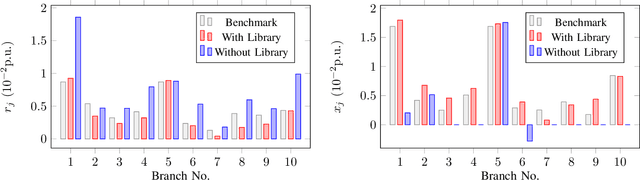
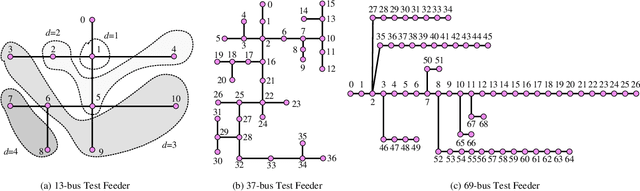
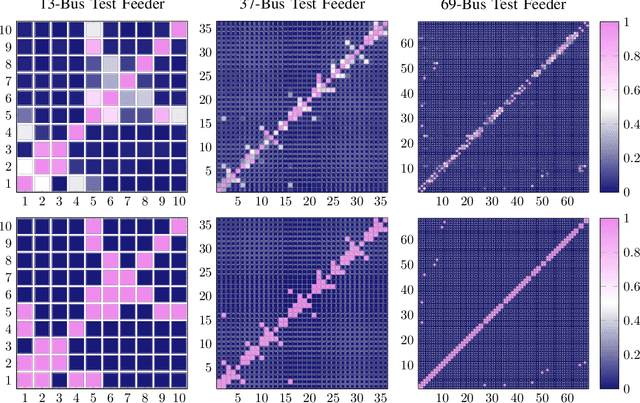
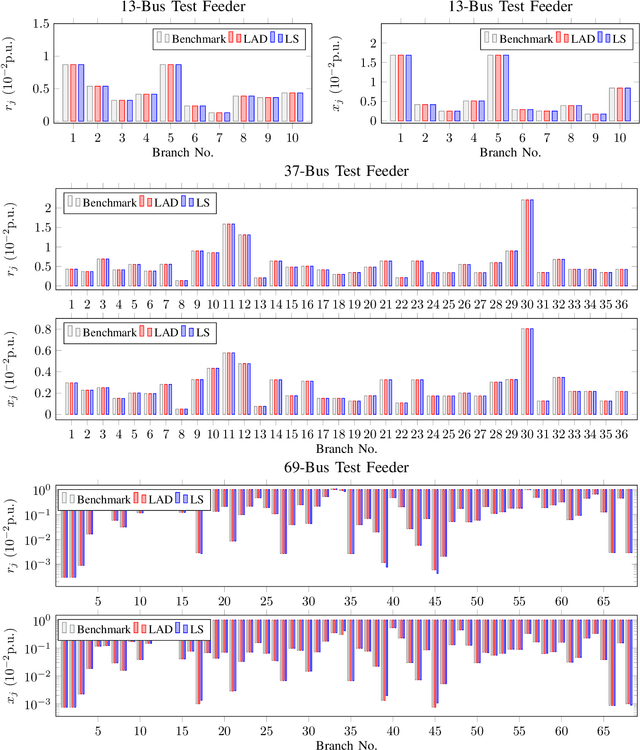
The knowledge of distribution grid models, including topologies and line impedances, is essential to grid monitoring, control and protection. However, this information is often unavailable, incomplete or outdated. The increasing deployment of smart meters (SMs) provides a unique opportunity to address this issue. This paper proposes a two-stage data-driven framework for distribution grid modeling using SM data. In the first stage, we propose to identify the topology via reconstructing a weighted Laplacian matrix of distribution networks, which is mathematically proven to be robust against moderately heterogeneous R/X profiles. In the second stage, we develop nonlinear least absolute deviations (LAD) and least squares (LS) regression models to estimate line impedances of single branches based on a nonlinear inverse power flow, which is then embedded within a bottom-up sweep algorithm to achieve the identification across the network in a branch-wise manner. Because the estimation models are inherently non-convex programs and NP-hard, we specially address their tractable convex relaxations and verify the exactness. In addition, we design a conductor library to significantly narrow down the solution space. Numerical results on the modified IEEE 13-bus, 37-bus and 69-bus test feeders validate the effectiveness of the proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge