Distribution-free risk assessment of regression-based machine learning algorithms
Paper and Code
Oct 05, 2023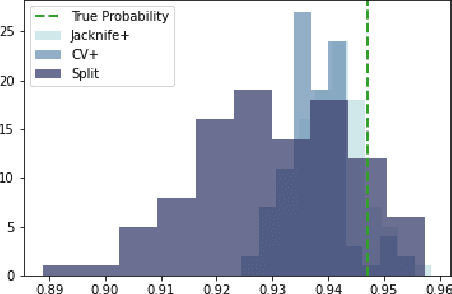
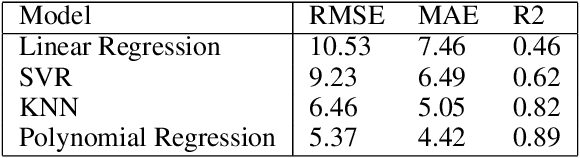
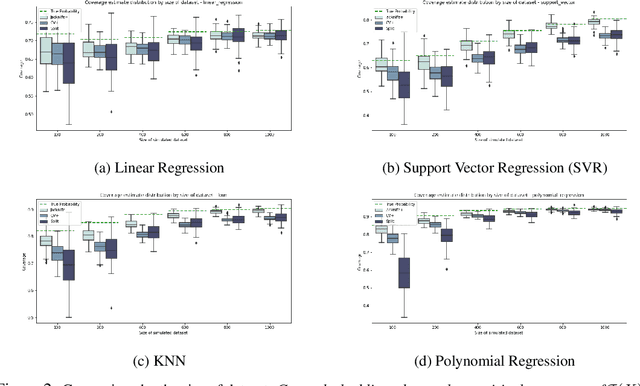
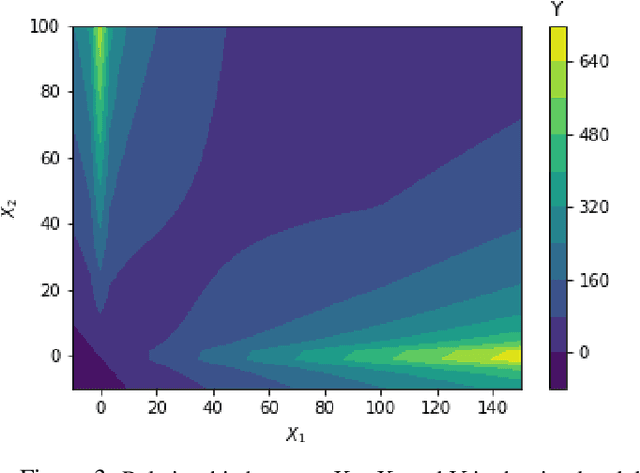
Machine learning algorithms have grown in sophistication over the years and are increasingly deployed for real-life applications. However, when using machine learning techniques in practical settings, particularly in high-risk applications such as medicine and engineering, obtaining the failure probability of the predictive model is critical. We refer to this problem as the risk-assessment task. We focus on regression algorithms and the risk-assessment task of computing the probability of the true label lying inside an interval defined around the model's prediction. We solve the risk-assessment problem using the conformal prediction approach, which provides prediction intervals that are guaranteed to contain the true label with a given probability. Using this coverage property, we prove that our approximated failure probability is conservative in the sense that it is not lower than the true failure probability of the ML algorithm. We conduct extensive experiments to empirically study the accuracy of the proposed method for problems with and without covariate shift. Our analysis focuses on different modeling regimes, dataset sizes, and conformal prediction methodologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge