Distributed Reinforcement Learning in Multi-Agent Networked Systems

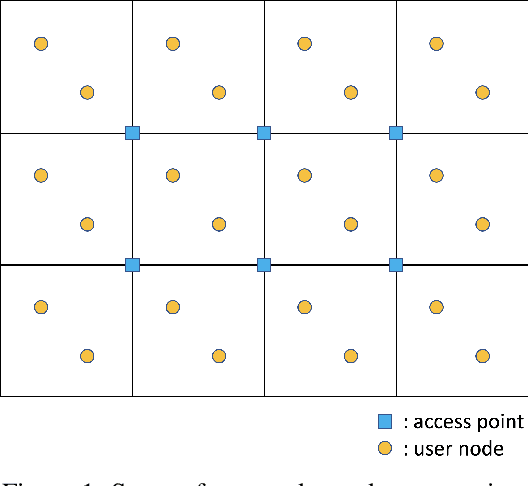
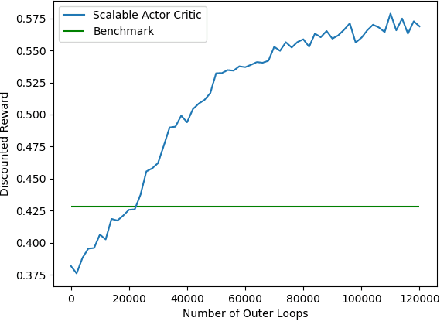
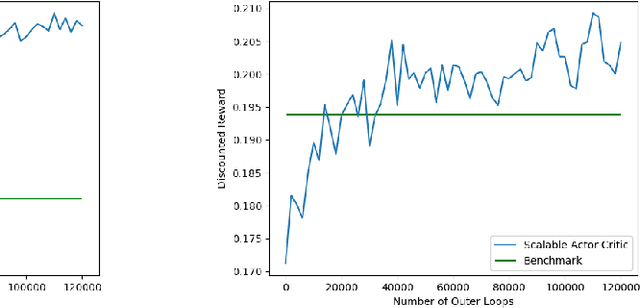
We study distributed reinforcement learning (RL) for a network of agents. The objective is to find localized policies that maximize the (discounted) global reward. In general, scalability is a challenge in this setting because the size of the global state/action space can be exponential in the number of agents. Scalable algorithms are only known in cases where dependencies are local, e.g., between neighbors. In this work, we propose a Scalable Actor Critic framework that applies in settings where the dependencies are non-local and provide a finite-time error bound that shows how the convergence rate depends on the depth of the dependencies in the network. Additionally, as a byproduct of our analysis, we obtain novel finite-time convergence results for a general stochastic approximation scheme and for temporal difference learning with state aggregation that apply beyond the setting of RL in networked systems.