Distributed Power Allocation with SINR Constraints Using Trial and Error Learning
Paper and Code
Feb 28, 2012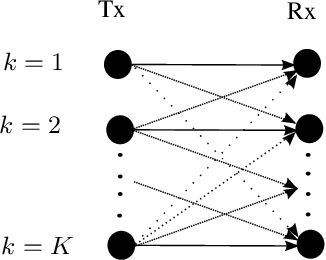
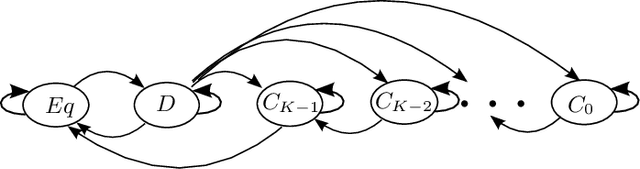
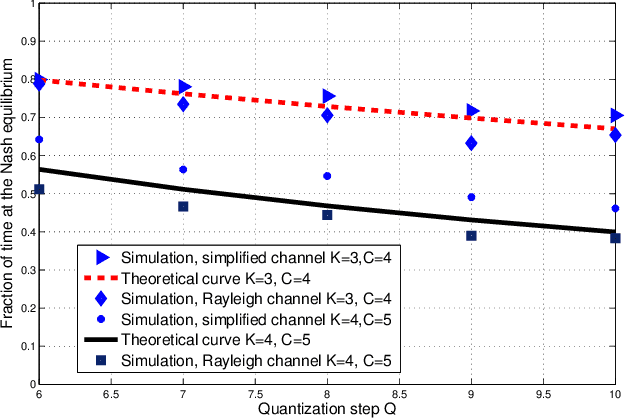
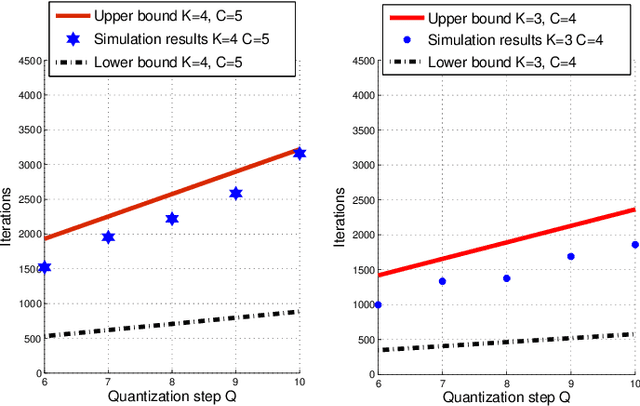
In this paper, we address the problem of global transmit power minimization in a self-congiguring network where radio devices are subject to operate at a minimum signal to interference plus noise ratio (SINR) level. We model the network as a parallel Gaussian interference channel and we introduce a fully decentralized algorithm (based on trial and error) able to statistically achieve a congiguration where the performance demands are met. Contrary to existing solutions, our algorithm requires only local information and can learn stable and efficient working points by using only one bit feedback. We model the network under two different game theoretical frameworks: normal form and satisfaction form. We show that the converging points correspond to equilibrium points, namely Nash and satisfaction equilibrium. Similarly, we provide sufficient conditions for the algorithm to converge in both formulations. Moreover, we provide analytical results to estimate the algorithm's performance, as a function of the network parameters. Finally, numerical results are provided to validate our theoretical conclusions. Keywords: Learning, power control, trial and error, Nash equilibrium, spectrum sharing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge