Distributed Invariant Kalman Filter for Cooperative Localization using Matrix Lie Groups
Paper and Code
May 07, 2024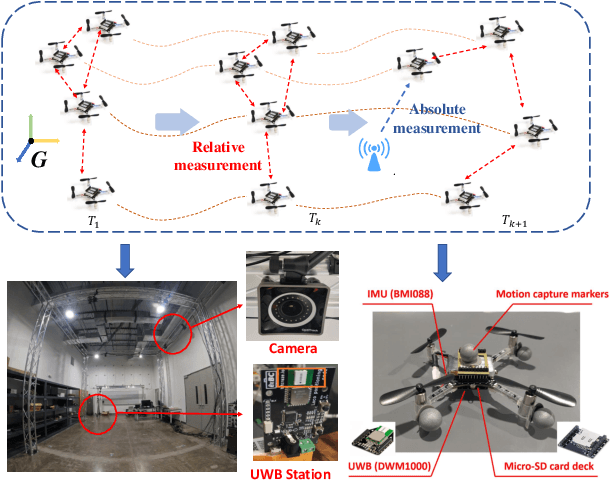
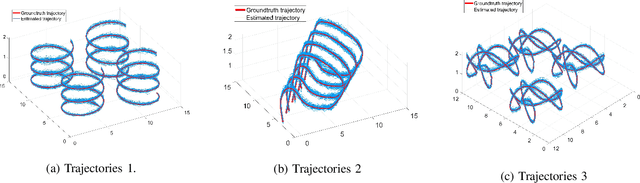
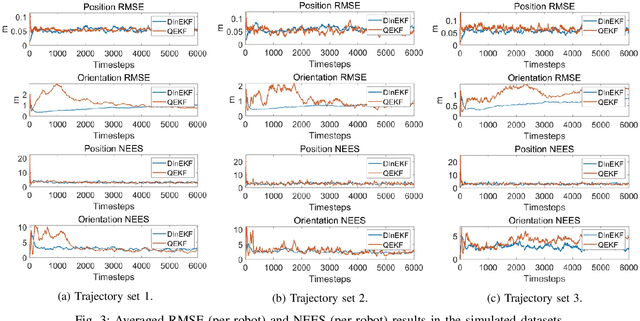
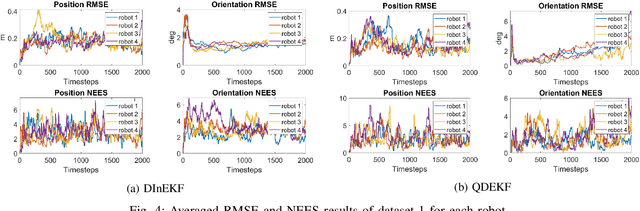
This paper studies the problem of Cooperative Localization (CL) for multi-robot systems, where a group of mobile robots jointly localize themselves by using measurements from onboard sensors and shared information from other robots. We propose a novel distributed invariant Kalman Filter (DInEKF) based on the Lie group theory, to solve the CL problem in a 3-D environment. Unlike the standard EKF which computes the Jacobians based on the linearization at the state estimate, DInEKF defines the robots' motion model on matrix Lie groups and offers the advantage of state estimate-independent Jacobians. This significantly improves the consistency of the estimator. Moreover, the proposed algorithm is fully distributed, relying solely on each robot's ego-motion measurements and information received from its one-hop communication neighbors. The effectiveness of the proposed algorithm is validated in both Monte-Carlo simulations and real-world experiments. The results show that the proposed DInEKF outperforms the standard distributed EKF in terms of both accuracy and consistency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge