Distributed Clustering of Linear Bandits in Peer to Peer Networks
Paper and Code
Jun 07, 2016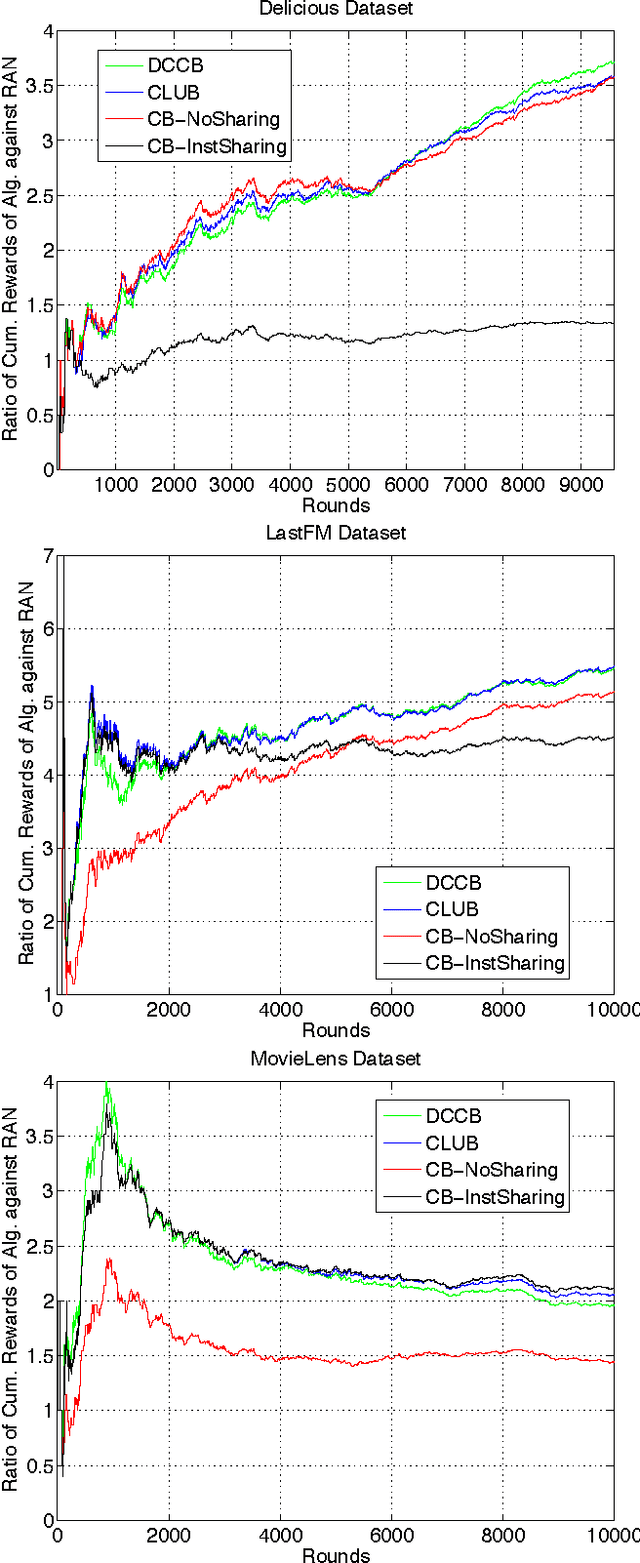
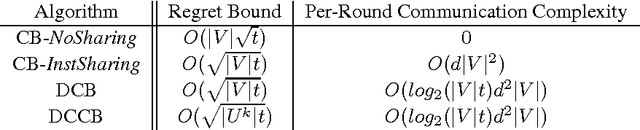
We provide two distributed confidence ball algorithms for solving linear bandit problems in peer to peer networks with limited communication capabilities. For the first, we assume that all the peers are solving the same linear bandit problem, and prove that our algorithm achieves the optimal asymptotic regret rate of any centralised algorithm that can instantly communicate information between the peers. For the second, we assume that there are clusters of peers solving the same bandit problem within each cluster, and we prove that our algorithm discovers these clusters, while achieving the optimal asymptotic regret rate within each one. Through experiments on several real-world datasets, we demonstrate the performance of proposed algorithms compared to the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge