Discriminative Optimization: Theory and Applications to Computer Vision Problems
Paper and Code
Jul 13, 2017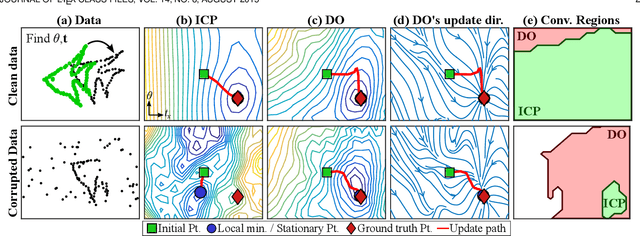
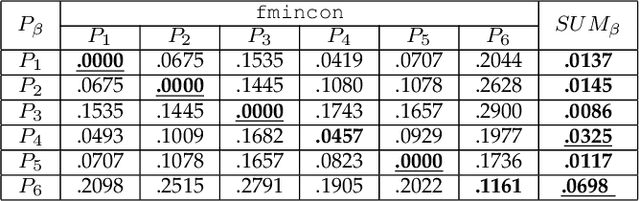
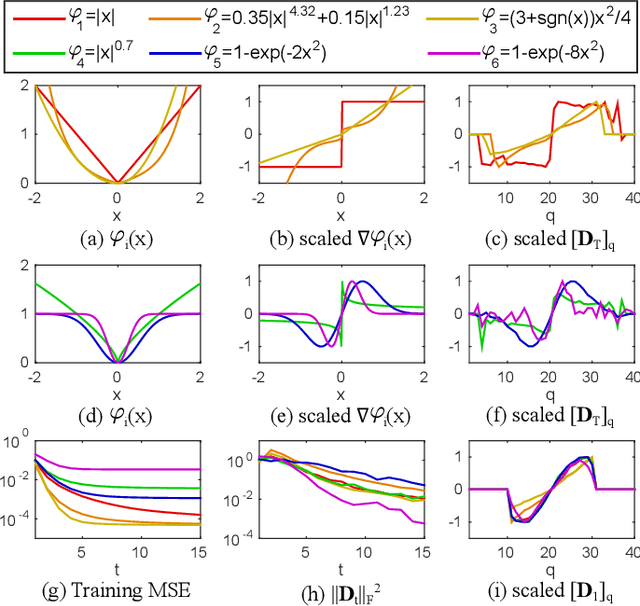
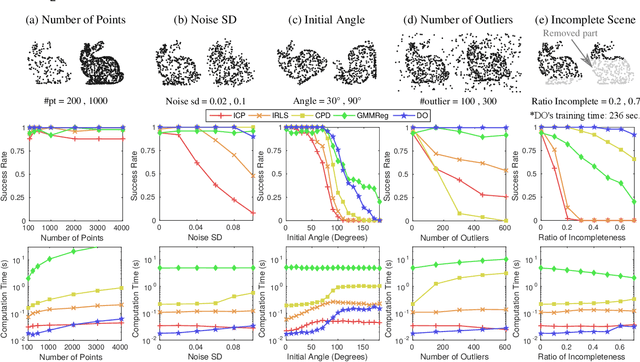
Many computer vision problems are formulated as the optimization of a cost function. This approach faces two main challenges: (i) designing a cost function with a local optimum at an acceptable solution, and (ii) developing an efficient numerical method to search for one (or multiple) of these local optima. While designing such functions is feasible in the noiseless case, the stability and location of local optima are mostly unknown under noise, occlusion, or missing data. In practice, this can result in undesirable local optima or not having a local optimum in the expected place. On the other hand, numerical optimization algorithms in high-dimensional spaces are typically local and often rely on expensive first or second order information to guide the search. To overcome these limitations, this paper proposes Discriminative Optimization (DO), a method that learns search directions from data without the need of a cost function. Specifically, DO explicitly learns a sequence of updates in the search space that leads to stationary points that correspond to desired solutions. We provide a formal analysis of DO and illustrate its benefits in the problem of 3D point cloud registration, camera pose estimation, and image denoising. We show that DO performed comparably or outperformed state-of-the-art algorithms in terms of accuracy, robustness to perturbations, and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge