Discrepancy-Based Active Learning for Domain Adaptation
Paper and Code
Mar 05, 2021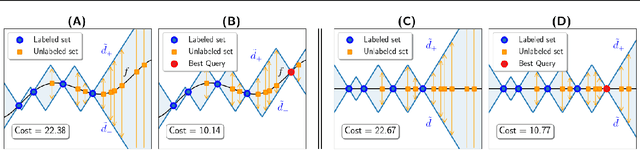
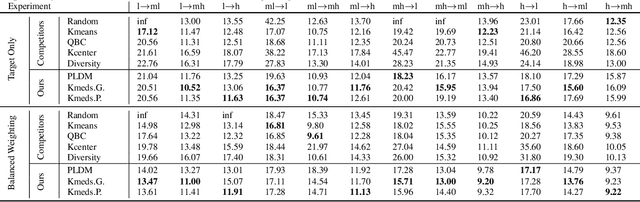
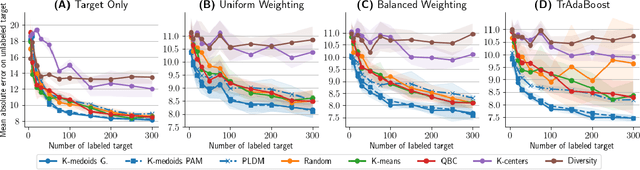
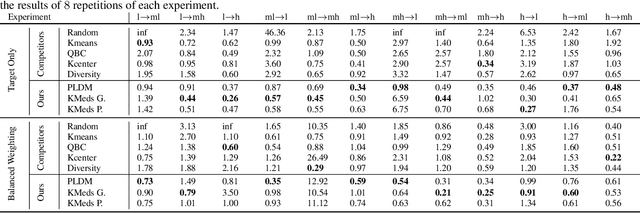
The goal of the paper is to design active learning strategies which lead to domain adaptation under an assumption of domain shift in the case of Lipschitz labeling function. Building on previous work by Mansour et al. (2009) we adapt the concept of discrepancy distance between source and target distributions to restrict the maximization over the hypothesis class to a localized class of functions which are performing accurate labeling on the source domain. We derive generalization error bounds for such active learning strategies in terms of Rademacher average and localized discrepancy for general loss functions which satisfy a regularity condition. Practical algorithms are inferred from the theoretical bounds, one is based on greedy optimization and the other is a K-medoids algorithm. We also provide improved versions of the algorithms to address the case of large data sets. These algorithms are competitive against other state-of-the-art active learning techniques in the context of domain adaptation as shown in our numerical experiments, in particular on large data sets of around one hundred thousand images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge