Discovering Power Laws in Entity Length

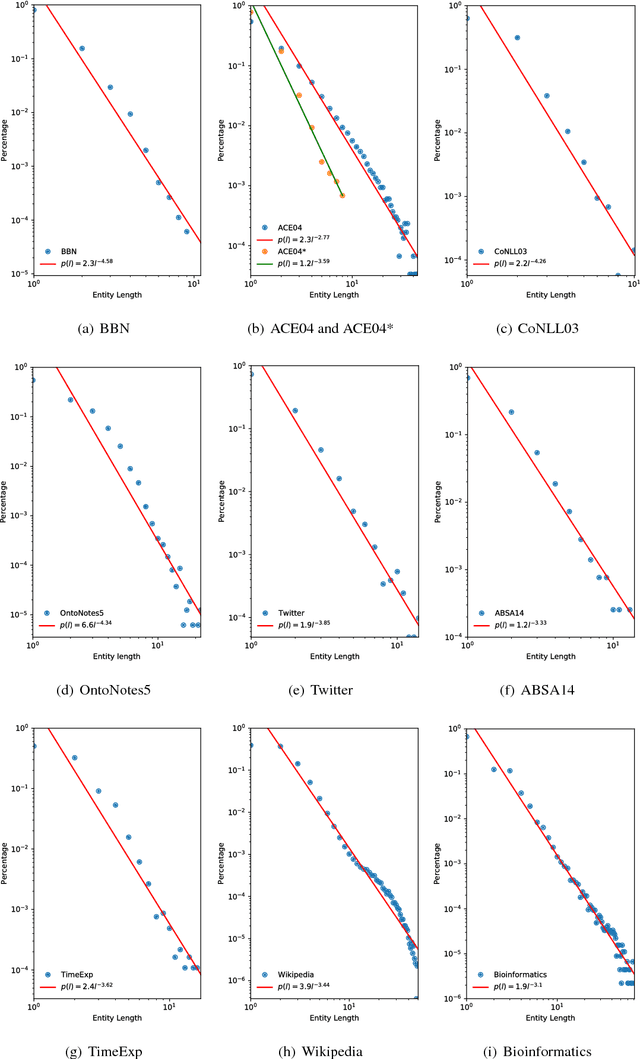
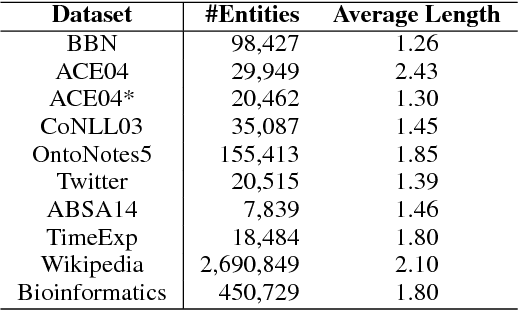
This paper presents a discovery that the length of the entities in various datasets follows a family of scale-free power law distributions. The concept of entity here broadly includes the named entity, entity mention, time expression, aspect term, and domain-specific entity that are well investigated in natural language processing and related areas. The entity length denotes the number of words in an entity. The power law distributions in entity length possess the scale-free property and have well-defined means and finite variances. We explain the phenomenon of power laws in entity length by the principle of least effort in communication and the preferential mechanism.