Directional Privacy for Deep Learning

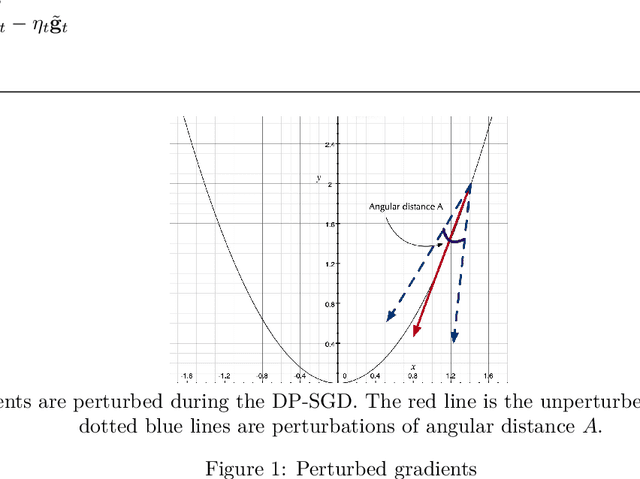
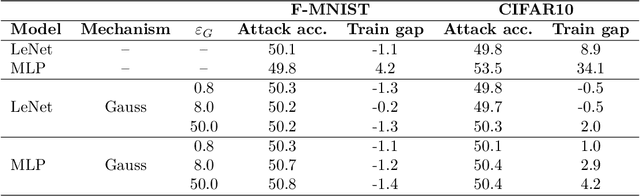
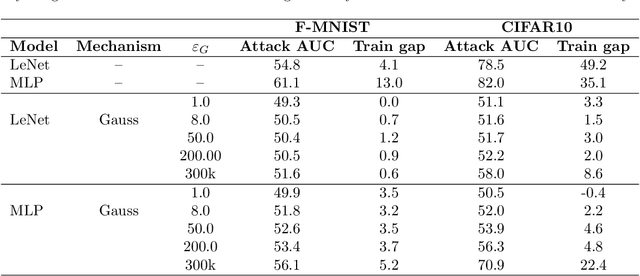
Differentially Private Stochastic Gradient Descent (DP-SGD) is a key method for applying privacy in the training of deep learning models. This applies isotropic Gaussian noise to gradients during training, which can perturb these gradients in any direction, damaging utility. Metric DP, however, can provide alternative mechanisms based on arbitrary metrics that might be more suitable. In this paper we apply \textit{directional privacy}, via a mechanism based on the von Mises-Fisher (VMF) distribution, to perturb gradients in terms of \textit{angular distance} so that gradient direction is broadly preserved. We show that this provides $\epsilon d$-privacy for deep learning training, rather than the $(\epsilon, \delta)$-privacy of the Gaussian mechanism; and that experimentally, on key datasets, the VMF mechanism can outperform the Gaussian in the utility-privacy trade-off.