Dimensionality's Blessing: Clustering Images by Underlying Distribution
Paper and Code
Apr 08, 2018

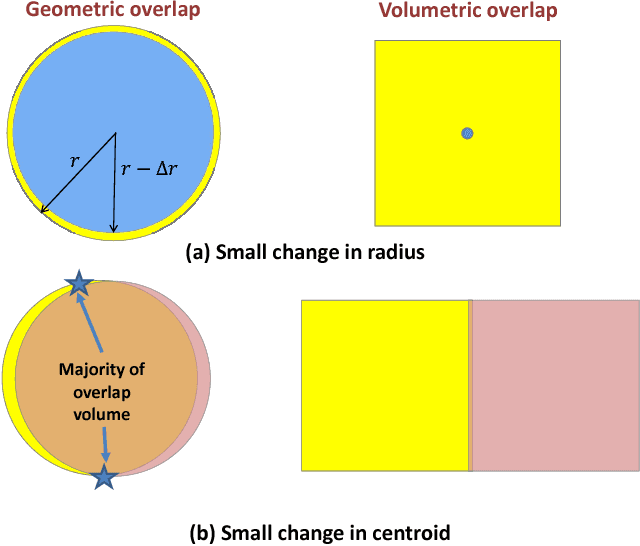
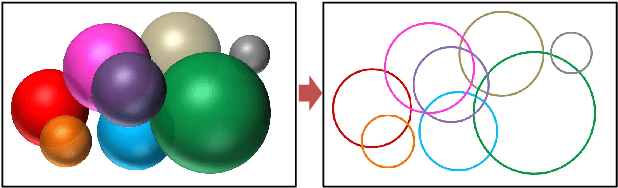
Many high dimensional vector distances tend to a constant. This is typically considered a negative "contrast-loss" phenomenon that hinders clustering and other machine learning techniques. We reinterpret "contrast-loss" as a blessing. Re-deriving "contrast-loss" using the law of large numbers, we show it results in a distribution's instances concentrating on a thin "hyper-shell". The hollow center means apparently chaotically overlapping distributions are actually intrinsically separable. We use this to develop distribution-clustering, an elegant algorithm for grouping of data points by their (unknown) underlying distribution. Distribution-clustering, creates notably clean clusters from raw unlabeled data, estimates the number of clusters for itself and is inherently robust to "outliers" which form their own clusters. This enables trawling for patterns in unorganized data and may be the key to enabling machine intelligence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge