Differentially Private Estimation of Heterogeneous Causal Effects
Paper and Code
Feb 22, 2022


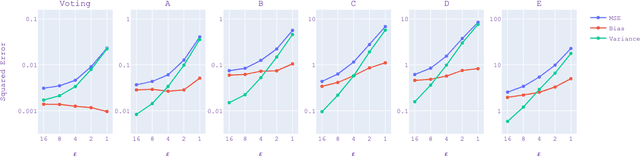
Estimating heterogeneous treatment effects in domains such as healthcare or social science often involves sensitive data where protecting privacy is important. We introduce a general meta-algorithm for estimating conditional average treatment effects (CATE) with differential privacy (DP) guarantees. Our meta-algorithm can work with simple, single-stage CATE estimators such as S-learner and more complex multi-stage estimators such as DR and R-learner. We perform a tight privacy analysis by taking advantage of sample splitting in our meta-algorithm and the parallel composition property of differential privacy. In this paper, we implement our approach using DP-EBMs as the base learner. DP-EBMs are interpretable, high-accuracy models with privacy guarantees, which allow us to directly observe the impact of DP noise on the learned causal model. Our experiments show that multi-stage CATE estimators incur larger accuracy loss than single-stage CATE or ATE estimators and that most of the accuracy loss from differential privacy is due to an increase in variance, not biased estimates of treatment effects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge