Differentially Private Data Releasing for Smooth Queries with Synthetic Database Output
Paper and Code
Jan 06, 2014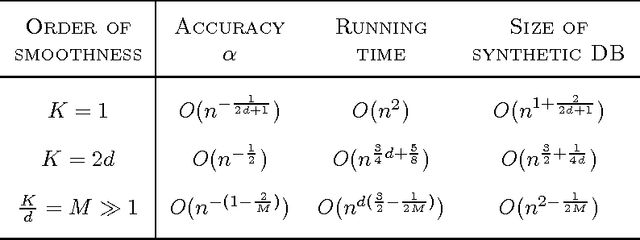
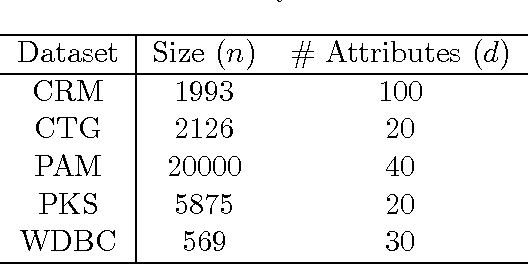
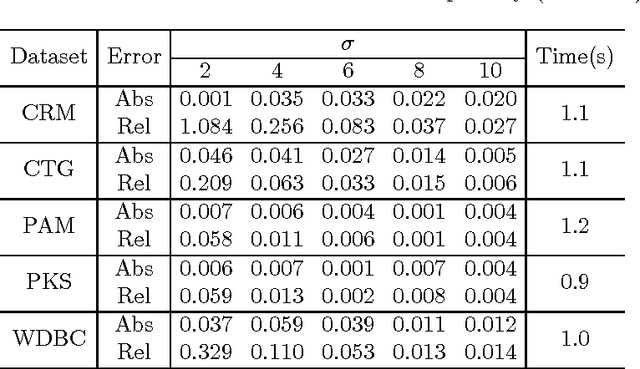
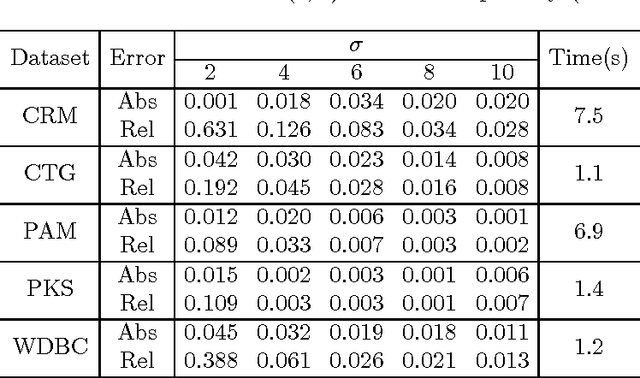
We consider accurately answering smooth queries while preserving differential privacy. A query is said to be $K$-smooth if it is specified by a function defined on $[-1,1]^d$ whose partial derivatives up to order $K$ are all bounded. We develop an $\epsilon$-differentially private mechanism for the class of $K$-smooth queries. The major advantage of the algorithm is that it outputs a synthetic database. In real applications, a synthetic database output is appealing. Our mechanism achieves an accuracy of $O (n^{-\frac{K}{2d+K}}/\epsilon )$, and runs in polynomial time. We also generalize the mechanism to preserve $(\epsilon, \delta)$-differential privacy with slightly improved accuracy. Extensive experiments on benchmark datasets demonstrate that the mechanisms have good accuracy and are efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge