Differential Privacy of Hierarchical Census Data: An Optimization Approach
Paper and Code
Jun 28, 2020
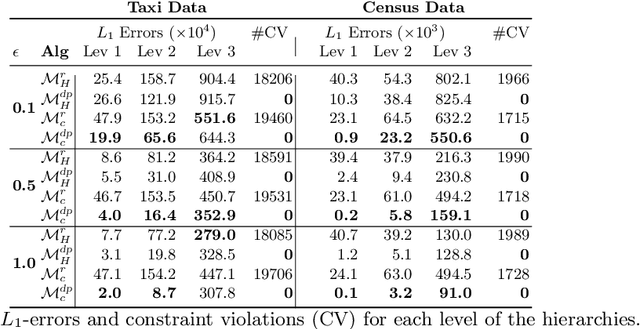
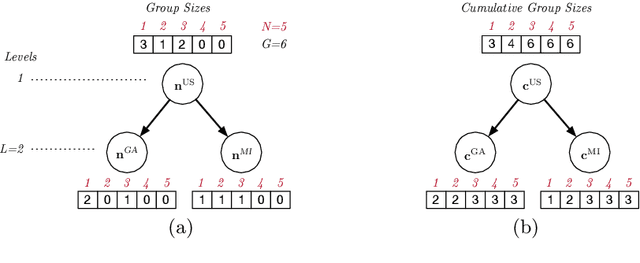

This paper is motivated by applications of a Census Bureau interested in releasing aggregate socio-economic data about a large population without revealing sensitive information about any individual. The released information can be the number of individuals living alone, the number of cars they own, or their salary brackets. Recent events have identified some of the privacy challenges faced by these organizations. To address them, this paper presents a novel differential-privacy mechanism for releasing hierarchical counts of individuals. The counts are reported at multiple granularities (e.g., the national, state, and county levels) and must be consistent across all levels. The core of the mechanism is an optimization model that redistributes the noise introduced to achieve differential privacy in order to meet the consistency constraints between the hierarchical levels. The key technical contribution of the paper shows that this optimization problem can be solved in polynomial time by exploiting the structure of its cost functions. Experimental results on very large, real datasets show that the proposed mechanism provides improvements of up to two orders of magnitude in terms of computational efficiency and accuracy with respect to other state-of-the-art techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge