Differentiable Neural Architecture Search via Proximal Iterations

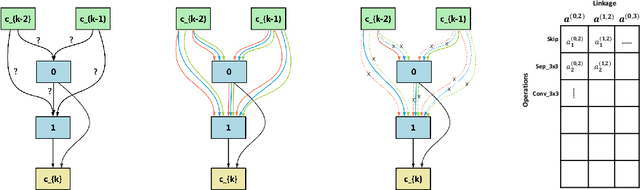
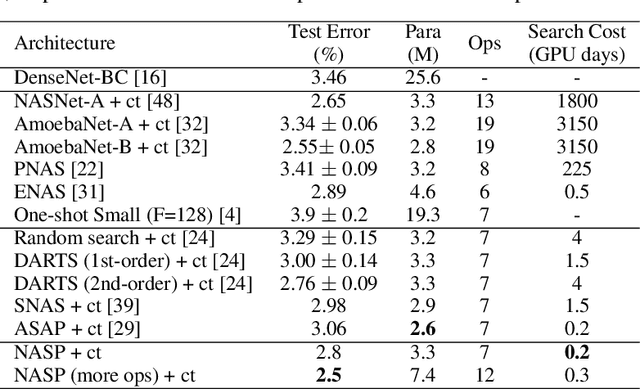
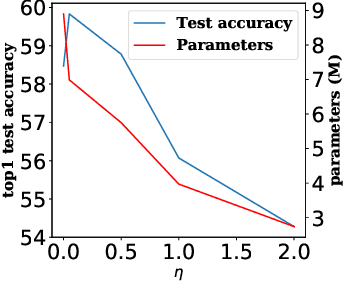
Neural architecture search (NAS) recently attracts much research attention because of its ability to identify better architectures than handcrafted ones. However, many NAS methods, which optimize the search process in a discrete search space, need many GPU days for convergence. Recently, DARTS, which constructs a differentiable search space and then optimizes it by gradient descent, can obtain high-performance architecture and reduces the search time to several days. However, DARTS is still slow as it updates an ensemble of all operations and keeps only one after convergence. Besides, DARTS can converge to inferior architectures due to the strong correlation among operations. In this paper, we propose a new differentiable Neural Architecture Search method based on Proximal gradient descent (denoted as NASP). Different from DARTS, NASP reformulates the search process as an optimization problem with a constraint that only one operation is allowed to be updated during forward and backward propagation. Since the constraint is hard to deal with, we propose a new algorithm inspired by proximal iterations to solve it. Experiments on various tasks demonstrate that NASP can obtain high-performance architectures with 10 times of speedup on the computational time than DARTS.