Differentiable Inductive Logic Programming for Structured Examples
Paper and Code
Mar 02, 2021
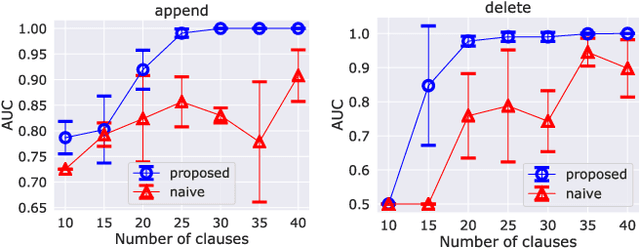
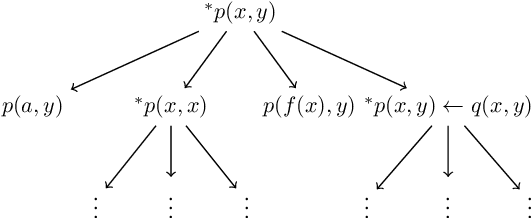
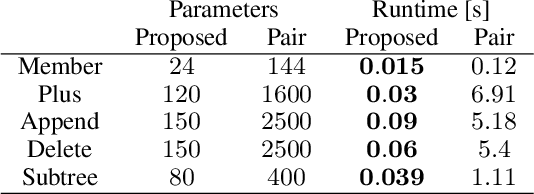
The differentiable implementation of logic yields a seamless combination of symbolic reasoning and deep neural networks. Recent research, which has developed a differentiable framework to learn logic programs from examples, can even acquire reasonable solutions from noisy datasets. However, this framework severely limits expressions for solutions, e.g., no function symbols are allowed, and the shapes of clauses are fixed. As a result, the framework cannot deal with structured examples. Therefore we propose a new framework to learn logic programs from noisy and structured examples, including the following contributions. First, we propose an adaptive clause search method by looking through structured space, which is defined by the generality of the clauses, to yield an efficient search space for differentiable solvers. Second, we propose for ground atoms an enumeration algorithm, which determines a necessary and sufficient set of ground atoms to perform differentiable inference functions. Finally, we propose a new method to compose logic programs softly, enabling the system to deal with complex programs consisting of several clauses. Our experiments show that our new framework can learn logic programs from noisy and structured examples, such as sequences or trees. Our framework can be scaled to deal with complex programs that consist of several clauses with function symbols.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge