Differentiable Combinatorial Scheduling at Scale
Paper and Code
Jun 06, 2024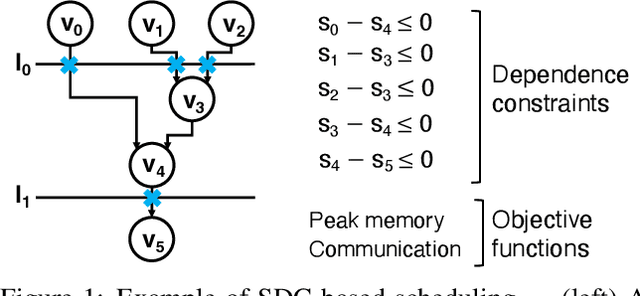
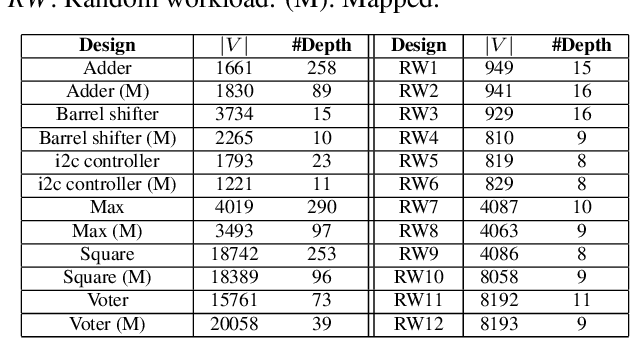
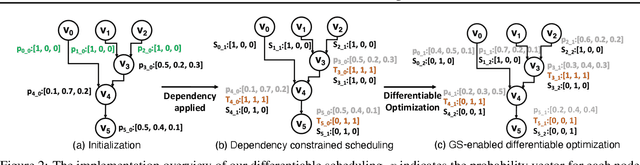
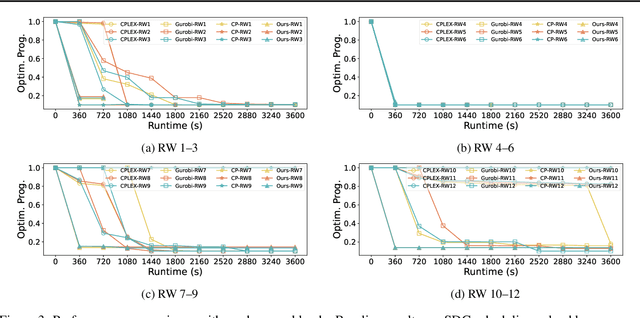
This paper addresses the complex issue of resource-constrained scheduling, an NP-hard problem that spans critical areas including chip design and high-performance computing. Traditional scheduling methods often stumble over scalability and applicability challenges. We propose a novel approach using a differentiable combinatorial scheduling framework, utilizing Gumbel-Softmax differentiable sampling technique. This new technical allows for a fully differentiable formulation of linear programming (LP) based scheduling, extending its application to a broader range of LP formulations. To encode inequality constraints for scheduling tasks, we introduce \textit{constrained Gumbel Trick}, which adeptly encodes arbitrary inequality constraints. Consequently, our method facilitates an efficient and scalable scheduling via gradient descent without the need for training data. Comparative evaluations on both synthetic and real-world benchmarks highlight our capability to significantly improve the optimization efficiency of scheduling, surpassing state-of-the-art solutions offered by commercial and open-source solvers such as CPLEX, Gurobi, and CP-SAT in the majority of the designs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge