Detecting Nonlinear Causality in Multivariate Time Series with Sparse Additive Models
Paper and Code
Apr 26, 2018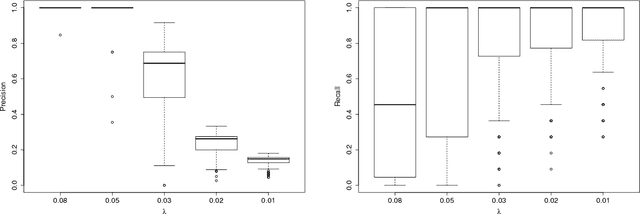
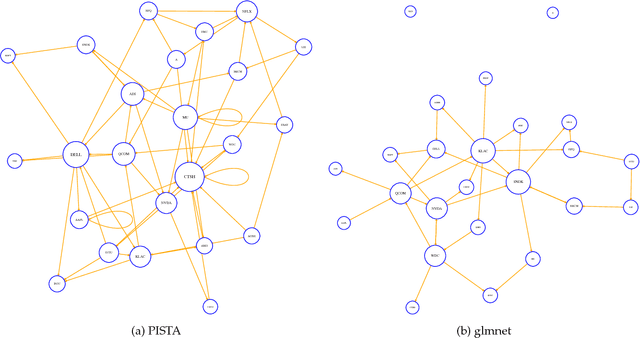
We propose a nonparametric method for detecting nonlinear causal relationship within a set of multidimensional discrete time series, by using sparse additive models (SpAMs). We show that, when the input to the SpAM is a $\beta$-mixing time series, the model can be fitted by first approximating each unknown function with a linear combination of a set of B-spline bases, and then solving a group-lasso-type optimization problem with nonconvex regularization. Theoretically, we characterize the oracle statistical properties of the proposed sparse estimator in function estimation and model selection. Numerically, we propose an efficient pathwise iterative shrinkage thresholding algorithm (PISTA), which tames the nonconvexity and guarantees linear convergence towards the desired sparse estimator with high probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge