Designing the Game to Play: Optimizing Payoff Structure in Security Games
Paper and Code
May 22, 2018
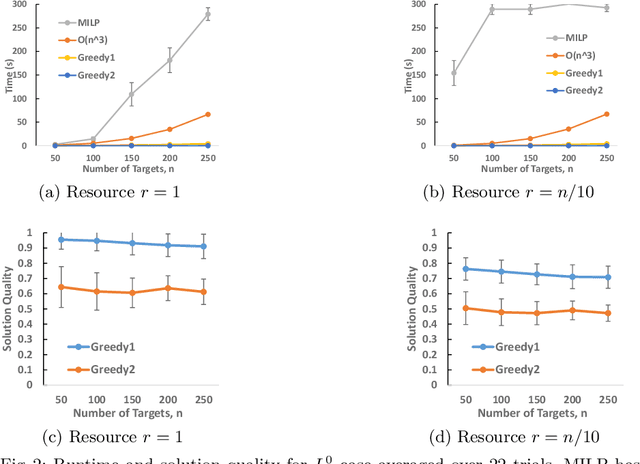
Effective game-theoretic modeling of defender-attacker behavior is becoming increasingly important. In many domains, the defender functions not only as a player but also the designer of the game's payoff structure. We study Stackelberg Security Games where the defender, in addition to allocating defensive resources to protect targets from the attacker, can strategically manipulate the attacker's payoff under budget constraints in weighted L^p-norm form regarding the amount of change. Focusing on problems with weighted L^1-norm form constraint, we present (i) a mixed integer linear program-based algorithm with approximation guarantee; (ii) a branch-and-bound based algorithm with improved efficiency achieved by effective pruning; (iii) a polynomial time approximation scheme for a special but practical class of problems. In addition, we show that problems under budget constraints in L^0-norm form and weighted L^\infty-norm form can be solved in polynomial time. We provide an extensive experimental evaluation of our proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge