Design of Supervision-Scalable Learning Systems: Methodology and Performance Benchmarking

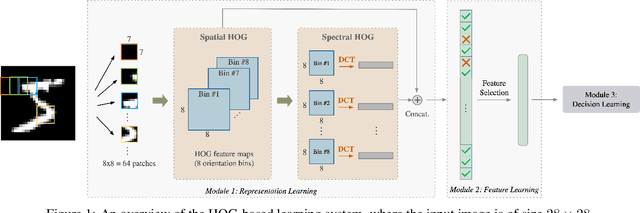
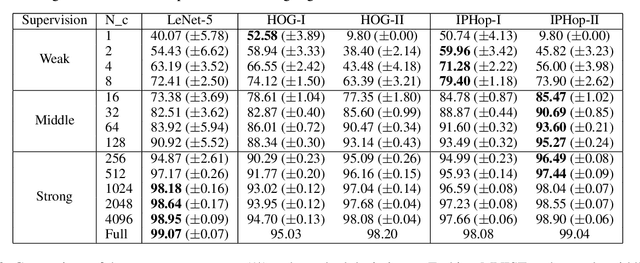
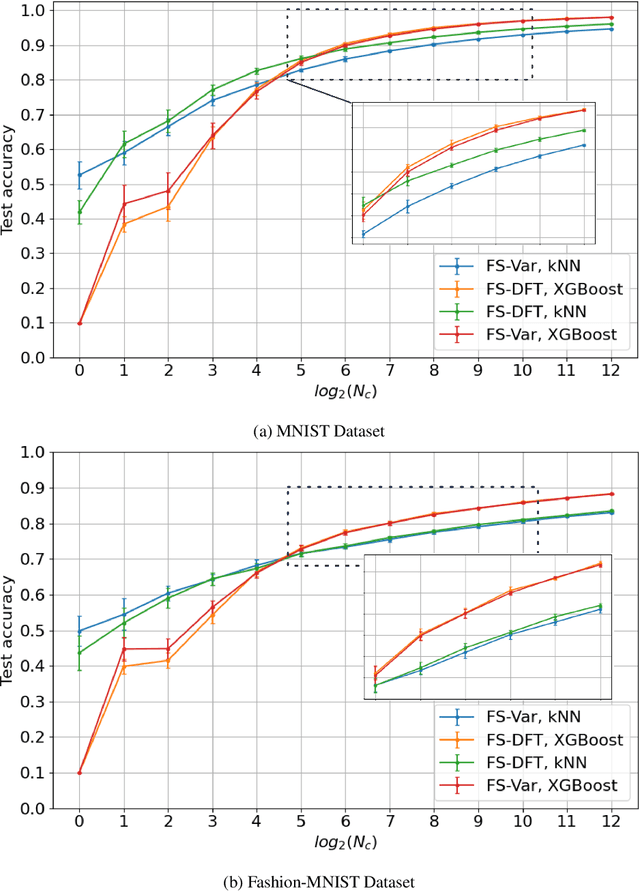
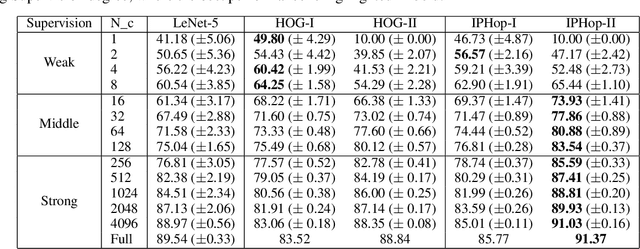
The design of robust learning systems that offer stable performance under a wide range of supervision degrees is investigated in this work. We choose the image classification problem as an illustrative example and focus on the design of modularized systems that consist of three learning modules: representation learning, feature learning and decision learning. We discuss ways to adjust each module so that the design is robust with respect to different training sample numbers. Based on these ideas, we propose two families of learning systems. One adopts the classical histogram of oriented gradients (HOG) features while the other uses successive-subspace-learning (SSL) features. We test their performance against LeNet-5, which is an end-to-end optimized neural network, for MNIST and Fashion-MNIST datasets. The number of training samples per image class goes from the extremely weak supervision condition (i.e., 1 labeled sample per class) to the strong supervision condition (i.e., 4096 labeled sample per class) with gradual transition in between (i.e., $2^n$, $n=0, 1, \cdots, 12$). Experimental results show that the two families of modularized learning systems have more robust performance than LeNet-5. They both outperform LeNet-5 by a large margin for small $n$ and have performance comparable with that of LeNet-5 for large $n$.