Design of MIMO Radar Waveforms based on lp-Norm Criteria
Paper and Code
Apr 07, 2021
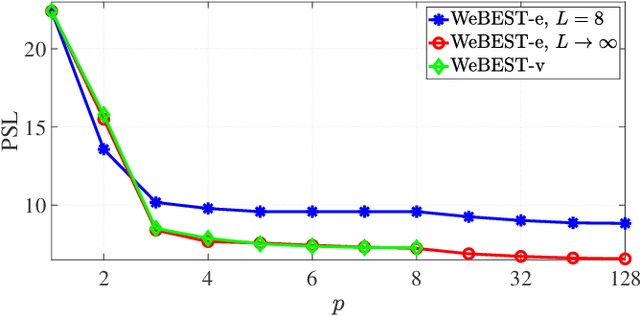
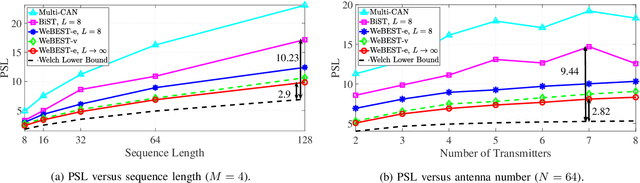

Multiple-input multiple-output (MIMO) radars transmit a set of sequences that exhibit small cross-correlation sidelobes, to enhance sensing performance by separating them at the matched filter outputs. The waveforms also require small auto-correlation sidelobes to avoid masking of weak targets by the range sidelobes of strong targets and to mitigate deleterious effects of distributed clutter. In light of these requirements, in this paper, we design a set of phase-only (constant modulus) sequences that exhibit near-optimal properties in terms of Peak Sidelobe Level (PSL) and Integrated Sidelobe Level (ISL). At the design stage, we adopt weighted lp-norm of auto- and cross-correlation sidelobes as the objective function and minimize it for a general p value, using block successive upper bound minimization (BSUM). Considering the limitation of radar amplifiers, we design unimodular sequences which make the design problem non-convex and NP-hard. To tackle the problem, in every iteration of the BSUM algorithm, we introduce different local approximation functions and optimize them concerning a block, containing a code entry or a code vector. The numerical results show that the performance of the optimized set of sequences outperforms the state-of-the-art counterparts, in both terms of PSL values and computational time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge