DeepPolar: Inventing Nonlinear Large-Kernel Polar Codes via Deep Learning
Paper and Code
Feb 14, 2024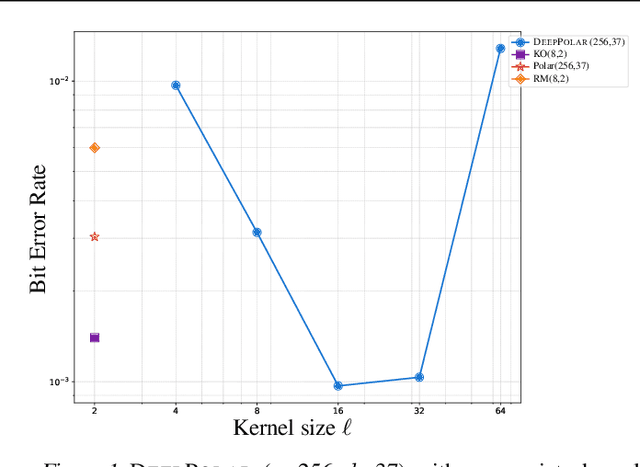

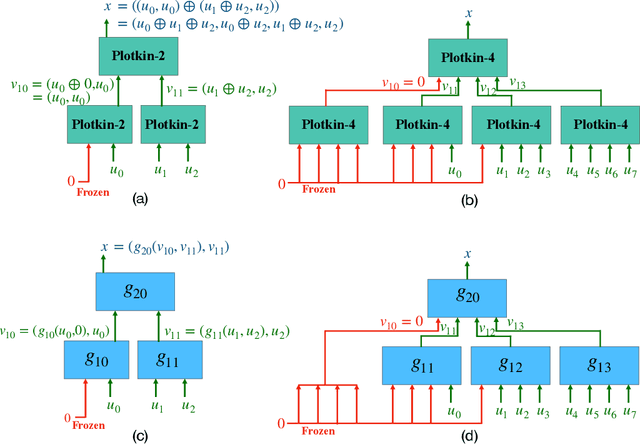
Polar codes, developed on the foundation of Arikan's polarization kernel, represent a breakthrough in coding theory and have emerged as the state-of-the-art error-correction-code in short-to-medium block length regimes. Importantly, recent research has indicated that the reliability of polar codes can be further enhanced by substituting Arikan's kernel with a larger one, leading to a faster polarization. However, for short-to-medium block length regimes, the development of polar codes that effectively employ large kernel sizes has not yet been realized. In this paper, we explore a novel, non-linear generalization of polar codes with an expanded kernel size, which we call DeepPolar codes. Our results show that DeepPolar codes effectively utilize the benefits of larger kernel size, resulting in enhanced reliability compared to both the existing neural codes and conventional polar codes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge