DeepMap: Learning Deep Representations for Graph Classification
Paper and Code
Apr 05, 2020
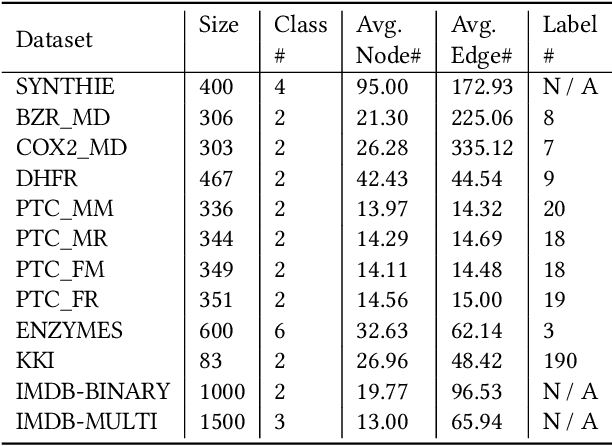
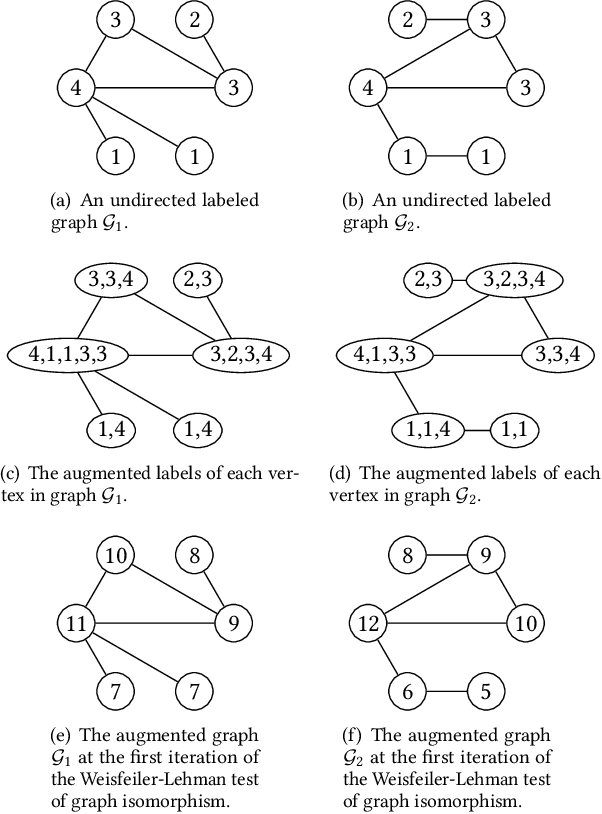
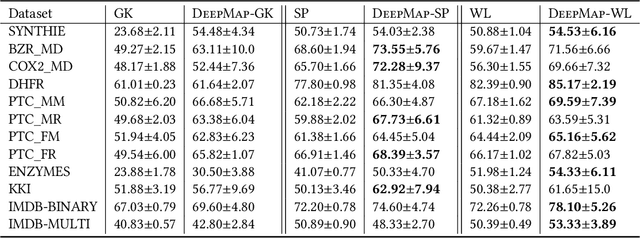
Graph-structured data arise in many scenarios. A fundamental problem is to quantify the similarities of graphs for tasks such as classification. Graph kernels are positive-semidefinite functions that decompose graphs into substructures and compare them. One problem in the effective implementation of this idea is that the substructures are not independent, which leads to high-dimensional feature space. In addition, graph kernels cannot capture the high-order complex interactions between vertices. To mitigate these two problems, we propose a framework called DeepMap to learn deep representations for graph feature maps. The learnt deep representation for a graph is a dense and low-dimensional vector that captures complex high-order interactions in a vertex neighborhood. DeepMap extends Convolutional Neural Networks (CNNs) to arbitrary graphs by aligning vertices across graphs and building the receptive field for each vertex. We empirically validate DeepMap on various graph classification benchmarks and demonstrate that it achieves state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge