Deep Sets
Paper and Code
Apr 14, 2018
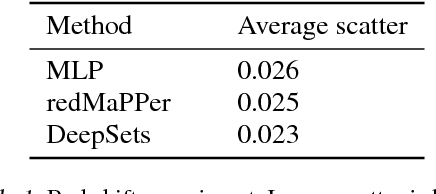
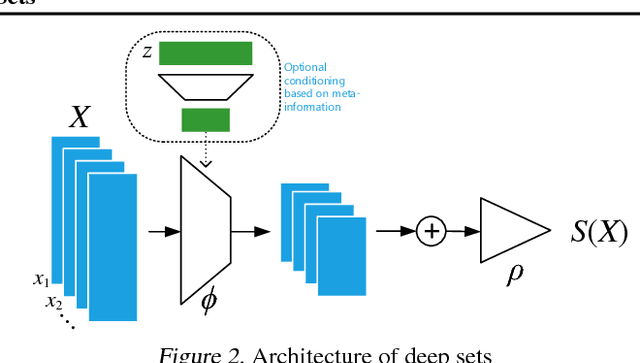
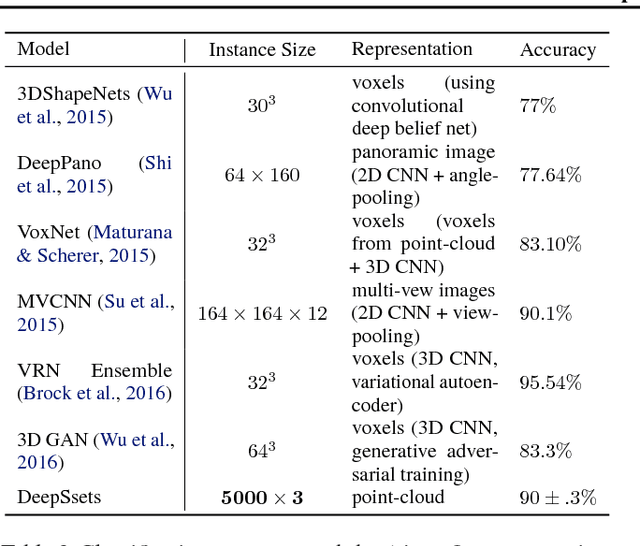
We study the problem of designing models for machine learning tasks defined on \emph{sets}. In contrast to traditional approach of operating on fixed dimensional vectors, we consider objective functions defined on sets that are invariant to permutations. Such problems are widespread, ranging from estimation of population statistics \cite{poczos13aistats}, to anomaly detection in piezometer data of embankment dams \cite{Jung15Exploration}, to cosmology \cite{Ntampaka16Dynamical,Ravanbakhsh16ICML1}. Our main theorem characterizes the permutation invariant functions and provides a family of functions to which any permutation invariant objective function must belong. This family of functions has a special structure which enables us to design a deep network architecture that can operate on sets and which can be deployed on a variety of scenarios including both unsupervised and supervised learning tasks. We also derive the necessary and sufficient conditions for permutation equivariance in deep models. We demonstrate the applicability of our method on population statistic estimation, point cloud classification, set expansion, and outlier detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge