Deep Point Set Resampling via Gradient Fields
Paper and Code
Nov 03, 2021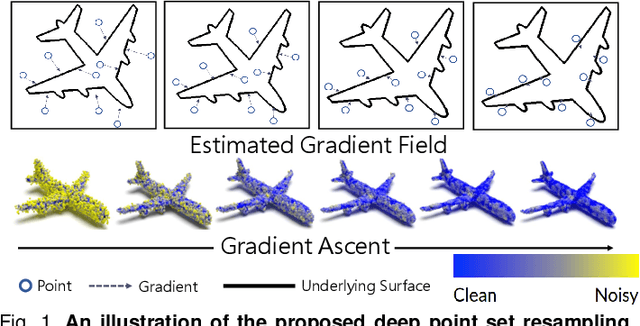
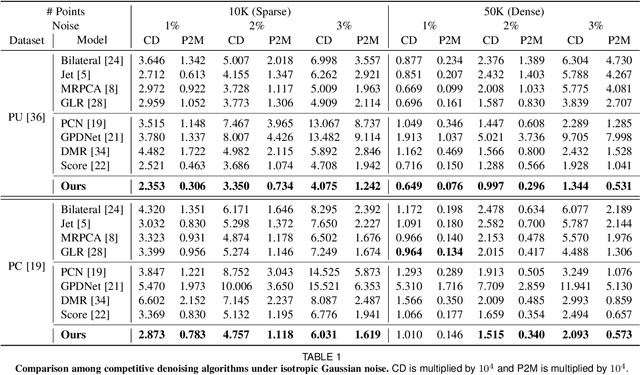
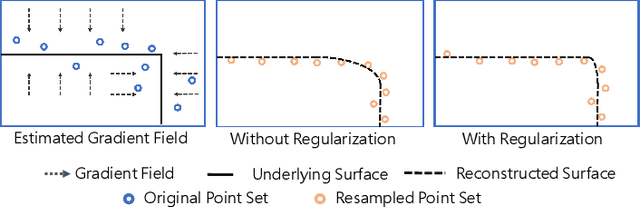
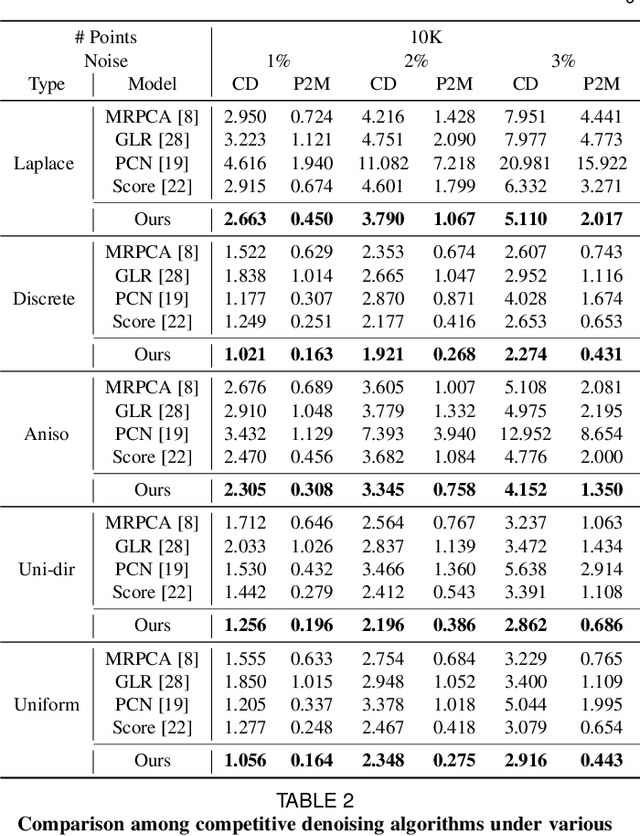
3D point clouds acquired by scanning real-world objects or scenes have found a wide range of applications including immersive telepresence, autonomous driving, surveillance, etc. They are often perturbed by noise or suffer from low density, which obstructs downstream tasks such as surface reconstruction and understanding. In this paper, we propose a novel paradigm of point set resampling for restoration, which learns continuous gradient fields of point clouds that converge points towards the underlying surface. In particular, we represent a point cloud via its gradient field -- the gradient of the log-probability density function, and enforce the gradient field to be continuous, thus guaranteeing the continuity of the model for solvable optimization. Based on the continuous gradient fields estimated via a proposed neural network, resampling a point cloud amounts to performing gradient-based Markov Chain Monte Carlo (MCMC) on the input noisy or sparse point cloud. Further, we propose to introduce regularization into the gradient-based MCMC during point cloud restoration, which essentially refines the intermediate resampled point cloud iteratively and accommodates various priors in the resampling process. Extensive experimental results demonstrate that the proposed point set resampling achieves the state-of-the-art performance in representative restoration tasks including point cloud denoising and upsampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge