Deep Neural Network for 3D Surface Segmentation based on Contour Tree Hierarchy
Paper and Code
Aug 25, 2020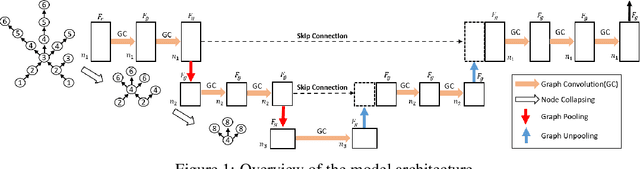
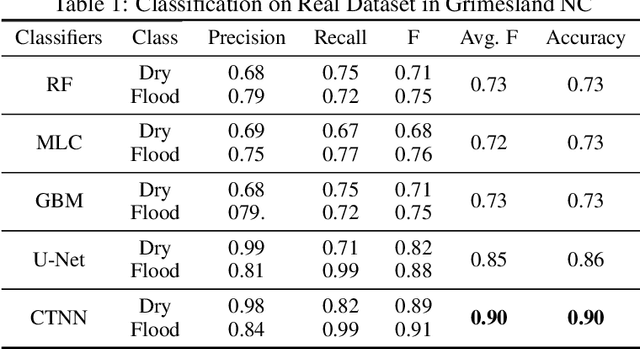
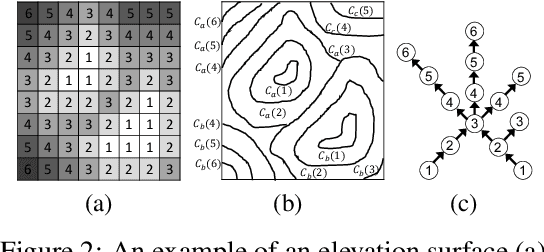
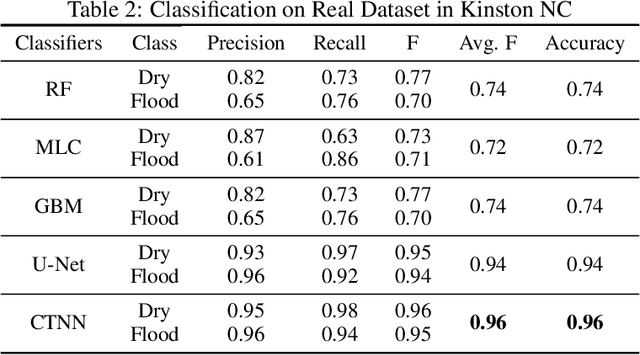
Given a 3D surface defined by an elevation function on a 2D grid as well as non-spatial features observed at each pixel, the problem of surface segmentation aims to classify pixels into contiguous classes based on both non-spatial features and surface topology. The problem has important applications in hydrology, planetary science, and biochemistry but is uniquely challenging for several reasons. First, the spatial extent of class segments follows surface contours in the topological space, regardless of their spatial shapes and directions. Second, the topological structure exists in multiple spatial scales based on different surface resolutions. Existing widely successful deep learning models for image segmentation are often not applicable due to their reliance on convolution and pooling operations to learn regular structural patterns on a grid. In contrast, we propose to represent surface topological structure by a contour tree skeleton, which is a polytree capturing the evolution of surface contours at different elevation levels. We further design a graph neural network based on the contour tree hierarchy to model surface topological structure at different spatial scales. Experimental evaluations based on real-world hydrological datasets show that our model outperforms several baseline methods in classification accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge