Deep learning as optimal control problems: models and numerical methods

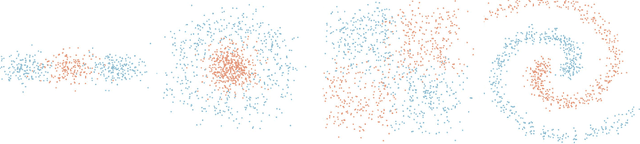
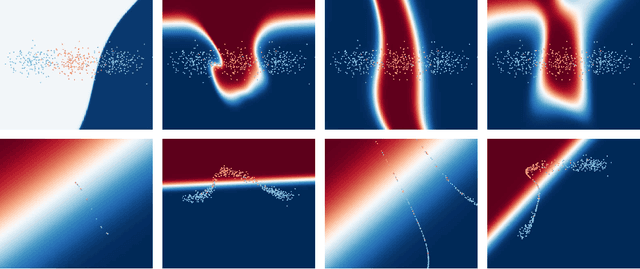
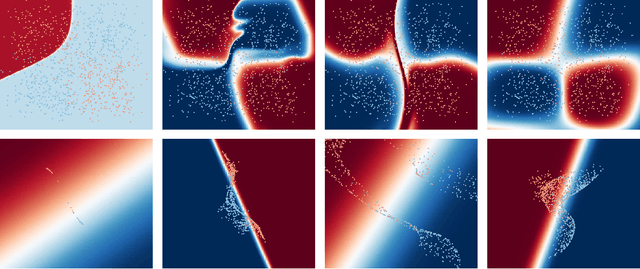
We consider recent work of Haber and Ruthotto 2017 and Chang et al. 2018, where deep learning neural networks have been interpreted as discretisations of an optimal control problem subject to an ordinary differential equation constraint. We review the first order conditions for optimality, and the conditions ensuring optimality after discretization. This leads to a class of algorithms for solving the discrete optimal control problem which guarantee that the corresponding discrete necessary conditions for optimality are fulfilled. We discuss two different deep learning algorithms and make a preliminary analysis of the ability of the algorithms to generalise.