Deep Latent Dirichlet Allocation with Topic-Layer-Adaptive Stochastic Gradient Riemannian MCMC
Paper and Code
Jun 06, 2017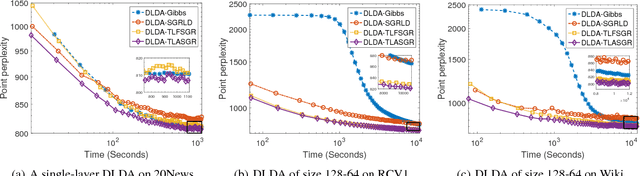
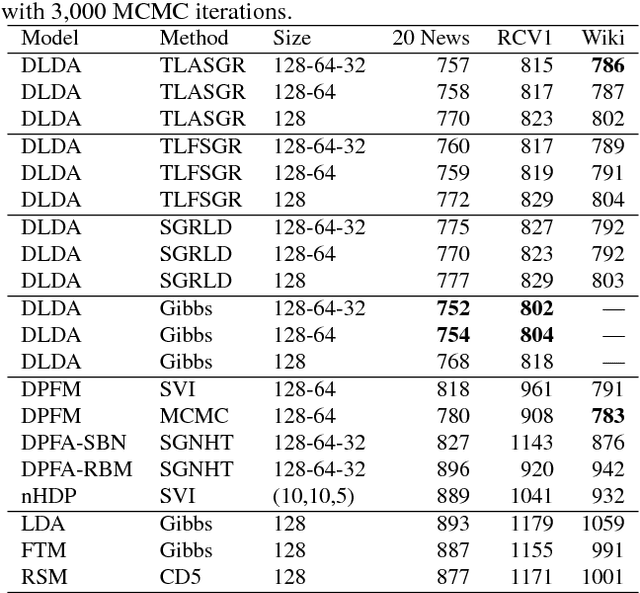
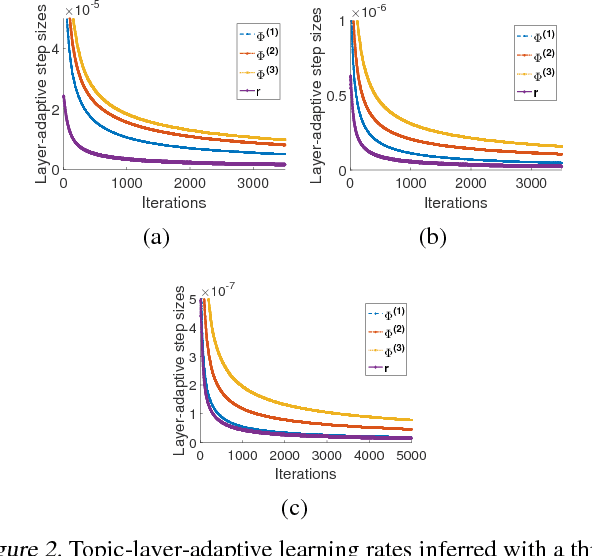
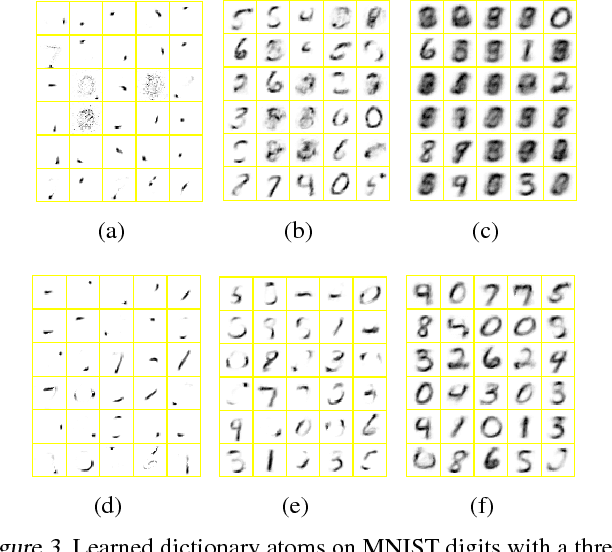
It is challenging to develop stochastic gradient based scalable inference for deep discrete latent variable models (LVMs), due to the difficulties in not only computing the gradients, but also adapting the step sizes to different latent factors and hidden layers. For the Poisson gamma belief network (PGBN), a recently proposed deep discrete LVM, we derive an alternative representation that is referred to as deep latent Dirichlet allocation (DLDA). Exploiting data augmentation and marginalization techniques, we derive a block-diagonal Fisher information matrix and its inverse for the simplex-constrained global model parameters of DLDA. Exploiting that Fisher information matrix with stochastic gradient MCMC, we present topic-layer-adaptive stochastic gradient Riemannian (TLASGR) MCMC that jointly learns simplex-constrained global parameters across all layers and topics, with topic and layer specific learning rates. State-of-the-art results are demonstrated on big data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge