Deep Geometric Learning with Monotonicity Constraints for Alzheimer's Disease Progression

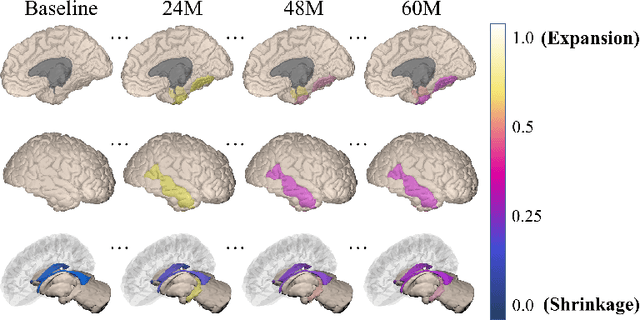
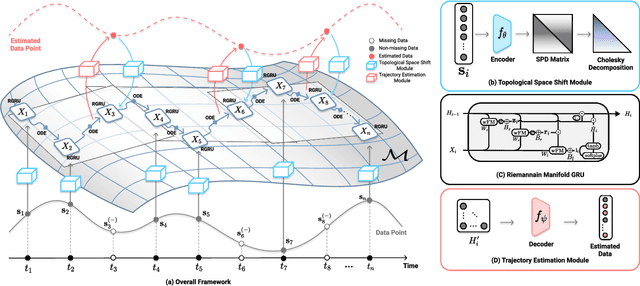
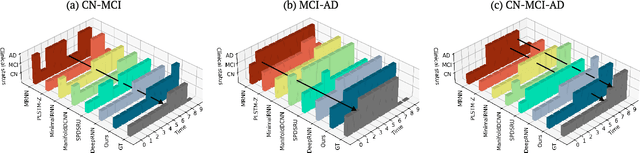
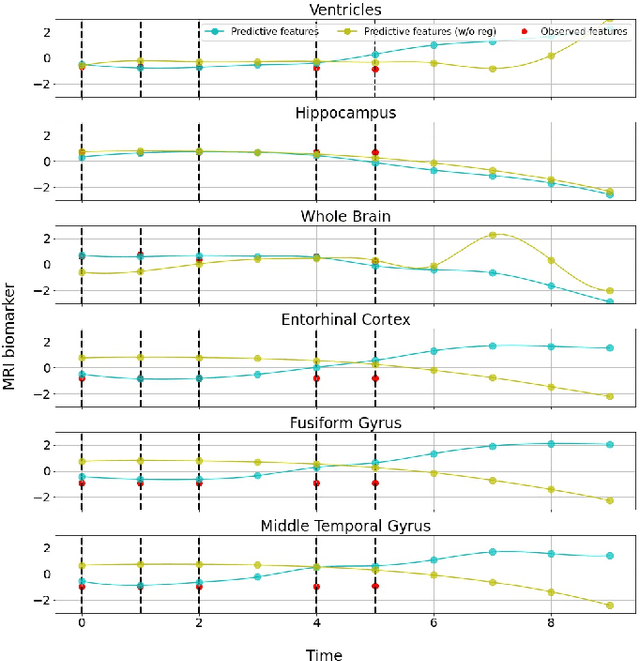
Alzheimer's disease (AD) is a devastating neurodegenerative condition that precedes progressive and irreversible dementia; thus, predicting its progression over time is vital for clinical diagnosis and treatment. Numerous studies have implemented structural magnetic resonance imaging (MRI) to model AD progression, focusing on three integral aspects: (i) temporal variability, (ii) incomplete observations, and (iii) temporal geometric characteristics. However, deep learning-based approaches regarding data variability and sparsity have yet to consider inherent geometrical properties sufficiently. The ordinary differential equation-based geometric modeling method (ODE-RGRU) has recently emerged as a promising strategy for modeling time-series data by intertwining a recurrent neural network and an ODE in Riemannian space. Despite its achievements, ODE-RGRU encounters limitations when extrapolating positive definite symmetric metrics from incomplete samples, leading to feature reverse occurrences that are particularly problematic, especially within the clinical facet. Therefore, this study proposes a novel geometric learning approach that models longitudinal MRI biomarkers and cognitive scores by combining three modules: topological space shift, ODE-RGRU, and trajectory estimation. We have also developed a training algorithm that integrates manifold mapping with monotonicity constraints to reflect measurement transition irreversibility. We verify our proposed method's efficacy by predicting clinical labels and cognitive scores over time in regular and irregular settings. Furthermore, we thoroughly analyze our proposed framework through an ablation study.