Decomposition of Uncertainty in Bayesian Deep Learning for Efficient and Risk-sensitive Learning
Paper and Code
Jun 15, 2018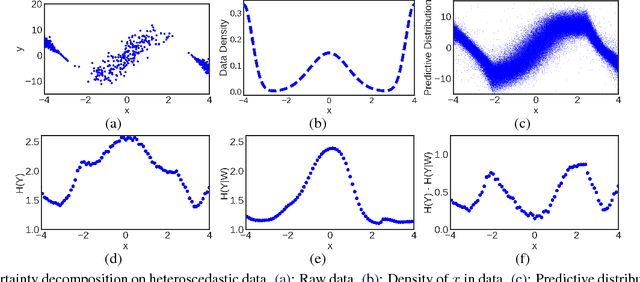

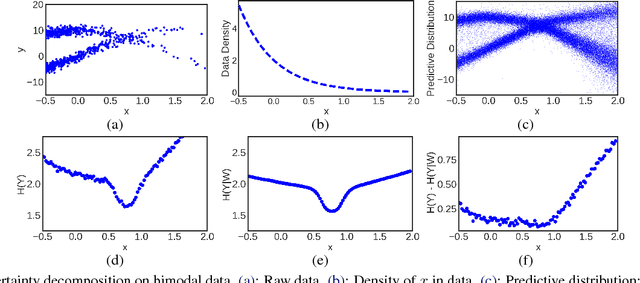
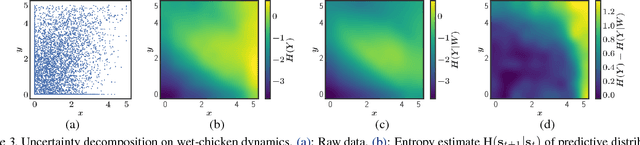
Bayesian neural networks with latent variables are scalable and flexible probabilistic models: They account for uncertainty in the estimation of the network weights and, by making use of latent variables, can capture complex noise patterns in the data. We show how to extract and decompose uncertainty into epistemic and aleatoric components for decision-making purposes. This allows us to successfully identify informative points for active learning of functions with heteroscedastic and bimodal noise. Using the decomposition we further define a novel risk-sensitive criterion for reinforcement learning to identify policies that balance expected cost, model-bias and noise aversion.
* This paper supersedes arXiv:1706.08495
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge