Decomposed Inductive Procedure Learning
Paper and Code
Oct 25, 2021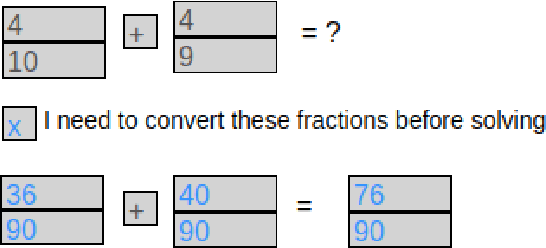
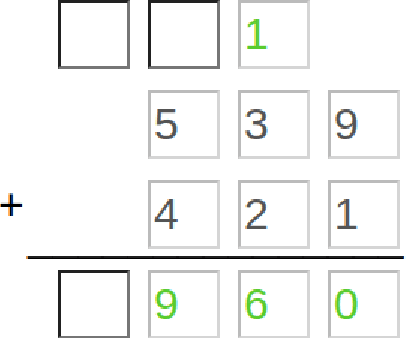
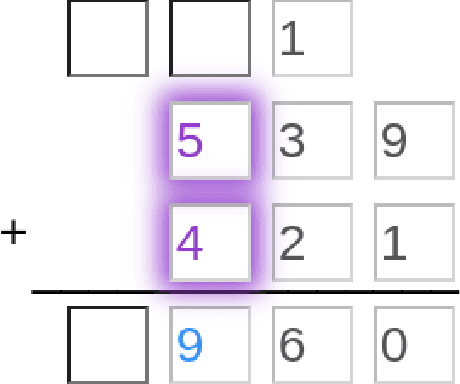
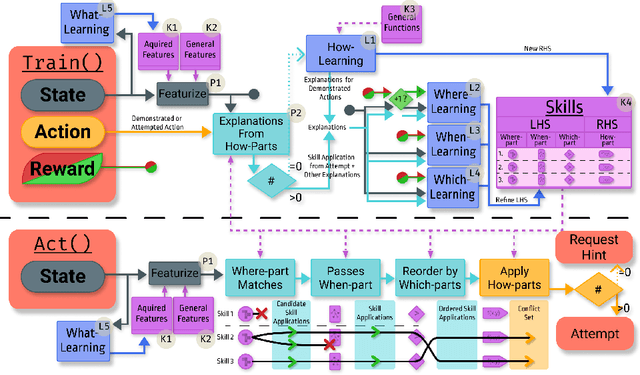
Recent advances in machine learning have made it possible to train artificially intelligent agents that perform with super-human accuracy on a great diversity of complex tasks. However, the process of training these capabilities often necessitates millions of annotated examples -- far more than humans typically need in order to achieve a passing level of mastery on similar tasks. Thus, while contemporary methods in machine learning can produce agents that exhibit super-human performance, their rate of learning per opportunity in many domains is decidedly lower than human-learning. In this work we formalize a theory of Decomposed Inductive Procedure Learning (DIPL) that outlines how different forms of inductive symbolic learning can be used in combination to build agents that learn educationally relevant tasks such as mathematical, and scientific procedures, at a rate similar to human learners. We motivate the construction of this theory along Marr's concepts of the computational, algorithmic, and implementation levels of cognitive modeling, and outline at the computational-level six learning capacities that must be achieved to accurately model human learning. We demonstrate that agents built along the DIPL theory are amenable to satisfying these capacities, and demonstrate, both empirically and theoretically, that DIPL enables the creation of agents that exhibit human-like learning performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge