Decentralized Personalized Federated Min-Max Problems
Paper and Code
Jun 14, 2021

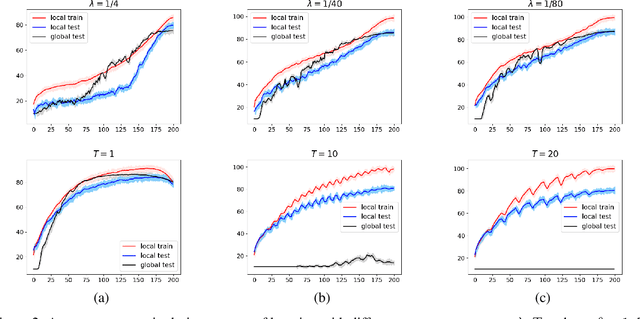
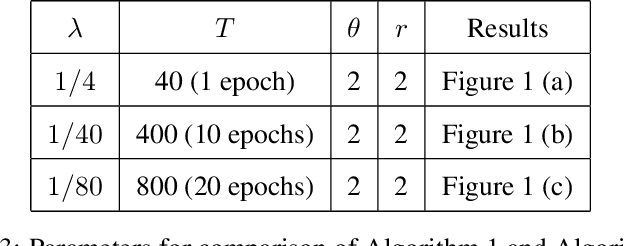
Personalized Federated Learning has recently seen tremendous progress, allowing the design of novel machine learning applications preserving privacy of the data used for training. Existing theoretical results in this field mainly focus on distributed optimization under minimization problems. This paper is the first to study PFL for saddle point problems, which cover a broader class of optimization tasks and are thus of more relevance for applications than the minimization. In this work, we consider a recently proposed PFL setting with the mixing objective function, an approach combining the learning of a global model together with local distributed learners. Unlike most of the previous papers, which considered only the centralized setting, we work in a more general and decentralized setup. This allows to design and to analyze more practical and federated ways to connect devices to the network. We present two new algorithms for our problem. A theoretical analysis of the methods is presented for smooth (strongly-)convex-(strongly-)concave saddle point problems. We also demonstrate the effectiveness of our problem formulation and the proposed algorithms on experiments with neural networks with adversarial noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge