Decentralized Optimization with Distributed Features and Non-Smooth Objective Functions
Paper and Code
Aug 23, 2022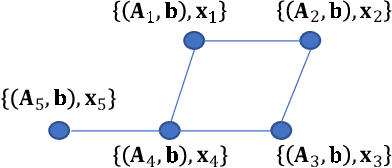
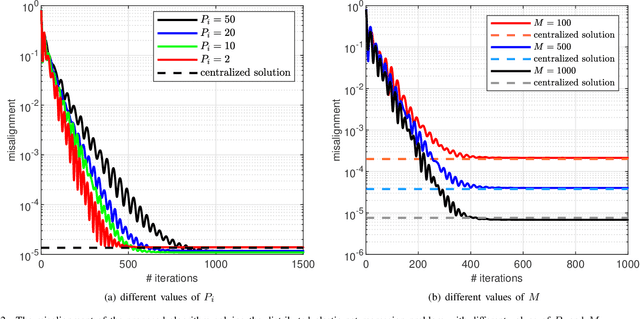
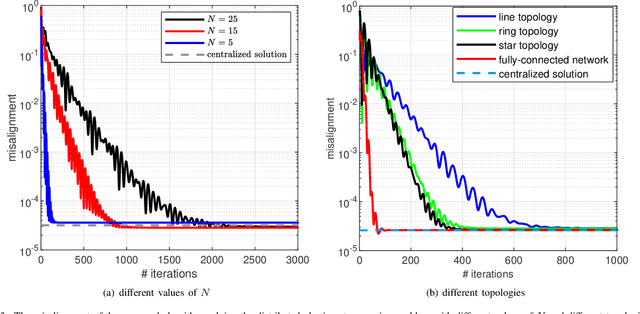
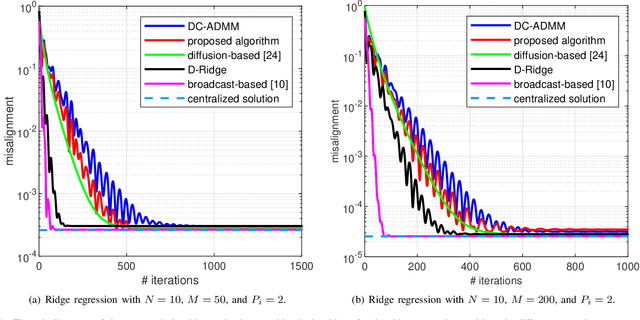
We develop a new consensus-based distributed algorithm for solving learning problems with feature partitioning and non-smooth convex objective functions. Such learning problems are not separable, i.e., the associated objective functions cannot be directly written as a summation of agent-specific objective functions. To overcome this challenge, we redefine the underlying optimization problem as a dual convex problem whose structure is suitable for distributed optimization using the alternating direction method of multipliers (ADMM). Next, we propose a new method to solve the minimization problem associated with the ADMM update step that does not rely on any conjugate function. Calculating the relevant conjugate functions may be hard or even unfeasible, especially when the objective function is non-smooth. To obviate computing any conjugate function, we solve the optimization problem associated with each ADMM iteration in the dual domain utilizing the block coordinate descent algorithm. Unlike the existing related algorithms, the proposed algorithm is fully distributed and does away with the conjugate of the objective function. We prove theoretically that the proposed algorithm attains the optimal centralized solution. We also confirm its network-wide convergence via simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge