Decentralized Online Learning: Take Benefits from Others' Data without Sharing Your Own to Track Global Trend

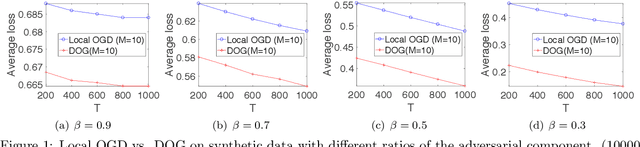
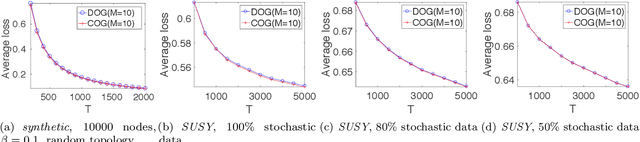
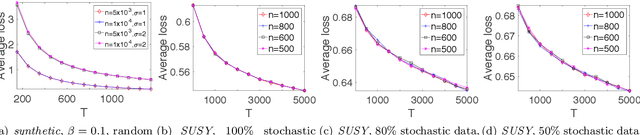
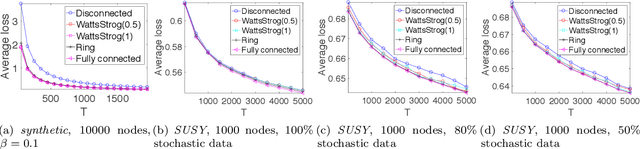
Decentralized Online Learning (online learning in decentralized networks) attracts more and more attention, since it is believed that Decentralized Online Learning can help the data providers cooperatively better solve their online problems without sharing their private data to a third party or other providers. Typically, the cooperation is achieved by letting the data providers exchange their models between neighbors, e.g., recommendation model. However, the best regret bound for a decentralized online learning algorithm is $\Ocal{n\sqrt{T}}$, where $n$ is the number of nodes (or users) and $T$ is the number of iterations. This is clearly insignificant since this bound can be achieved \emph{without} any communication in the networks. This reminds us to ask a fundamental question: \emph{Can people really get benefit from the decentralized online learning by exchanging information?} In this paper, we studied when and why the communication can help the decentralized online learning to reduce the regret. Specifically, each loss function is characterized by two components: the adversarial component and the stochastic component. Under this characterization, we show that decentralized online gradient (DOG) enjoys a regret bound $\Ocal{n\sqrt{T}G + \sqrt{nT}\sigma}$, where $G$ measures the magnitude of the adversarial component in the private data (or equivalently the local loss function) and $\sigma$ measures the randomness within the private data. This regret suggests that people can get benefits from the randomness in the private data by exchanging private information. Another important contribution of this paper is to consider the dynamic regret -- a more practical regret to track users' interest dynamics. Empirical studies are also conducted to validate our analysis.