De-biasing "bias" measurement
Paper and Code
May 11, 2022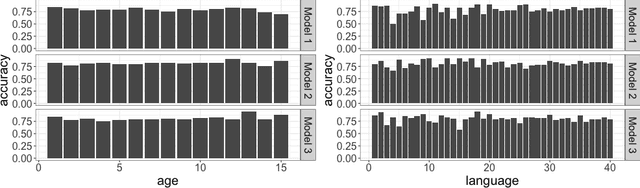

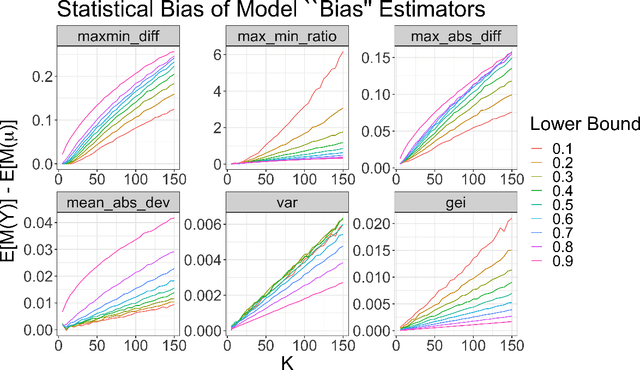
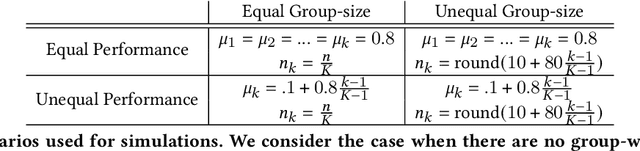
When a model's performance differs across socially or culturally relevant groups--like race, gender, or the intersections of many such groups--it is often called "biased." While much of the work in algorithmic fairness over the last several years has focused on developing various definitions of model fairness (the absence of group-wise model performance disparities) and eliminating such "bias," much less work has gone into rigorously measuring it. In practice, it important to have high quality, human digestible measures of model performance disparities and associated uncertainty quantification about them that can serve as inputs into multi-faceted decision-making processes. In this paper, we show both mathematically and through simulation that many of the metrics used to measure group-wise model performance disparities are themselves statistically biased estimators of the underlying quantities they purport to represent. We argue that this can cause misleading conclusions about the relative group-wise model performance disparities along different dimensions, especially in cases where some sensitive variables consist of categories with few members. We propose the "double-corrected" variance estimator, which provides unbiased estimates and uncertainty quantification of the variance of model performance across groups. It is conceptually simple and easily implementable without statistical software package or numerical optimization. We demonstrate the utility of this approach through simulation and show on a real dataset that while statistically biased estimators of model group-wise model performance disparities indicate statistically significant between-group model performance disparities, when accounting for statistical bias in the estimator, the estimated group-wise disparities in model performance are no longer statistically significant.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge