Datamodels: Predicting Predictions from Training Data
Paper and Code
Feb 01, 2022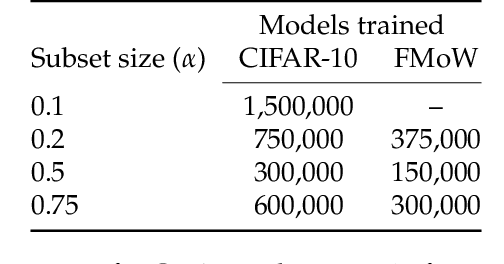


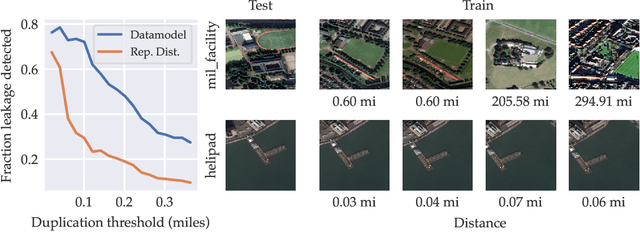
We present a conceptual framework, datamodeling, for analyzing the behavior of a model class in terms of the training data. For any fixed "target" example $x$, training set $S$, and learning algorithm, a datamodel is a parameterized function $2^S \to \mathbb{R}$ that for any subset of $S' \subset S$ -- using only information about which examples of $S$ are contained in $S'$ -- predicts the outcome of training a model on $S'$ and evaluating on $x$. Despite the potential complexity of the underlying process being approximated (e.g., end-to-end training and evaluation of deep neural networks), we show that even simple linear datamodels can successfully predict model outputs. We then demonstrate that datamodels give rise to a variety of applications, such as: accurately predicting the effect of dataset counterfactuals; identifying brittle predictions; finding semantically similar examples; quantifying train-test leakage; and embedding data into a well-behaved and feature-rich representation space. Data for this paper (including pre-computed datamodels as well as raw predictions from four million trained deep neural networks) is available at https://github.com/MadryLab/datamodels-data .
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge