Data-heterogeneity-aware Mixing for Decentralized Learning
Paper and Code
Apr 13, 2022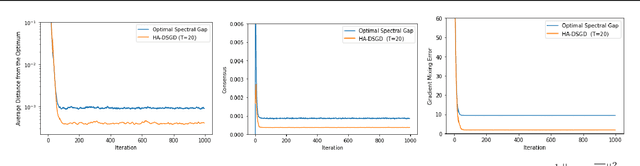
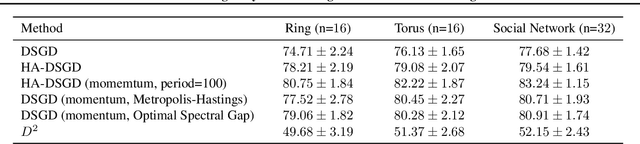
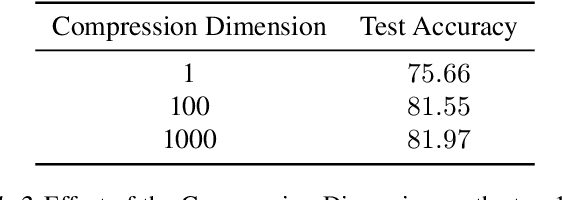
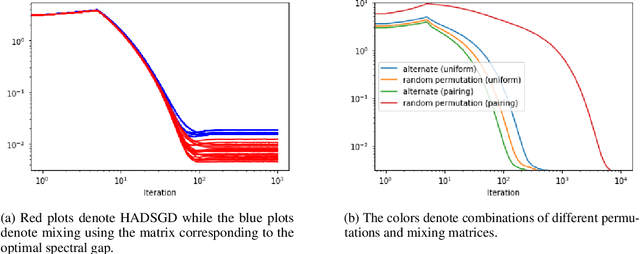
Decentralized learning provides an effective framework to train machine learning models with data distributed over arbitrary communication graphs. However, most existing approaches toward decentralized learning disregard the interaction between data heterogeneity and graph topology. In this paper, we characterize the dependence of convergence on the relationship between the mixing weights of the graph and the data heterogeneity across nodes. We propose a metric that quantifies the ability of a graph to mix the current gradients. We further prove that the metric controls the convergence rate, particularly in settings where the heterogeneity across nodes dominates the stochasticity between updates for a given node. Motivated by our analysis, we propose an approach that periodically and efficiently optimizes the metric using standard convex constrained optimization and sketching techniques. Through comprehensive experiments on standard computer vision and NLP benchmarks, we show that our approach leads to improvement in test performance for a wide range of tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge