Data-Driven Interpolation for Super-Scarce X-Ray Computed Tomography
Paper and Code
May 16, 2022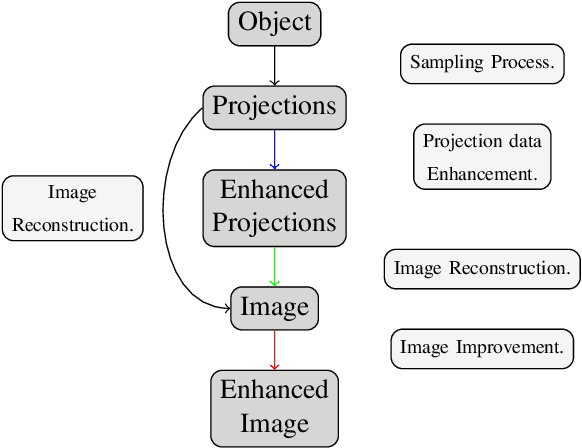
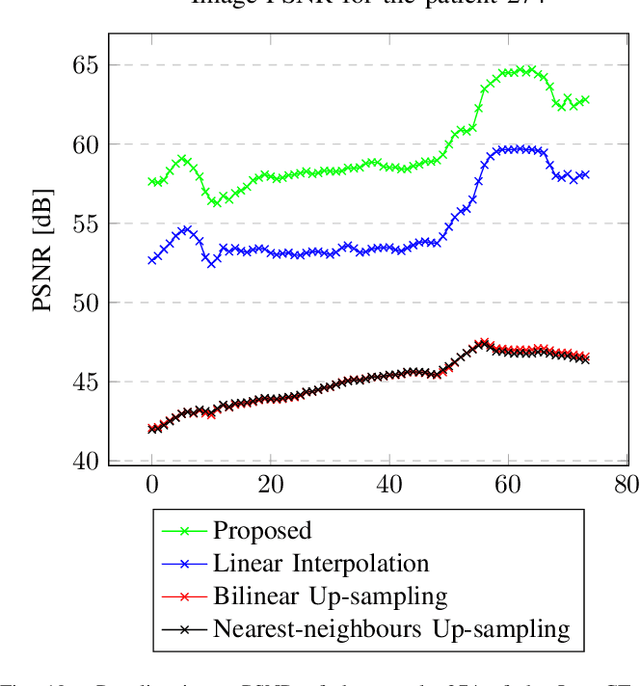
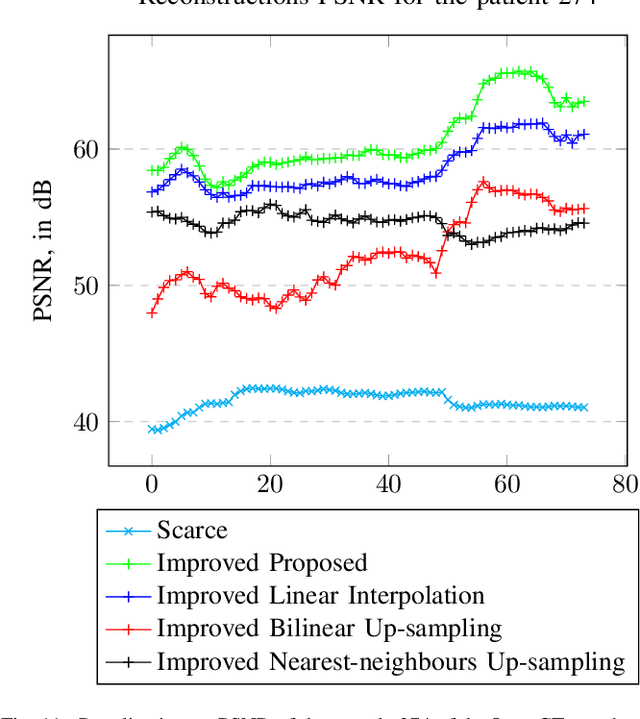
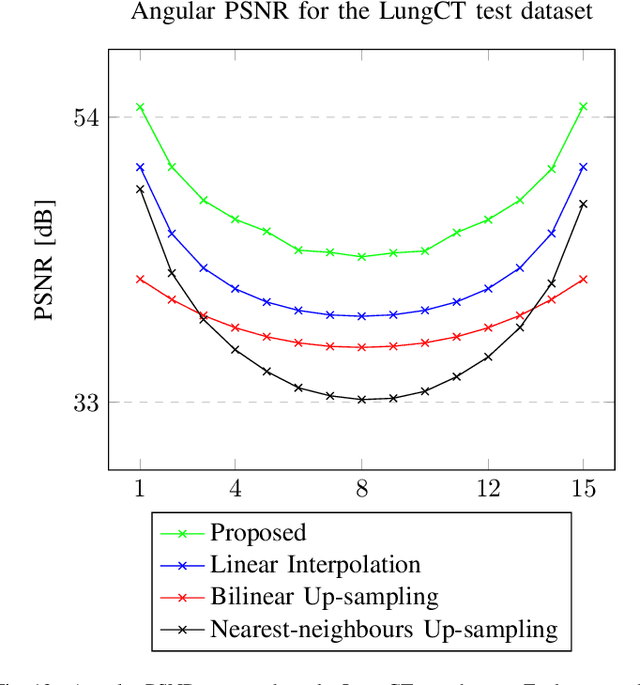
We address the problem of reconstructing X-Ray tomographic images from scarce measurements by interpolating missing acquisitions using a self-supervised approach. To do so, we train shallow neural networks to combine two neighbouring acquisitions into an estimated measurement at an intermediate angle. This procedure yields an enhanced sequence of measurements that can be reconstructed using standard methods, or further enhanced using regularisation approaches. Unlike methods that improve the sequence of acquisitions using an initial deterministic interpolation followed by machine-learning enhancement, we focus on inferring one measurement at once. This allows the method to scale to 3D, the computation to be faster and crucially, the interpolation to be significantly better than the current methods, when they exist. We also establish that a sequence of measurements must be processed as such, rather than as an image or a volume. We do so by comparing interpolation and up-sampling methods, and find that the latter significantly under-perform. We compare the performance of the proposed method against deterministic interpolation and up-sampling procedures and find that it outperforms them, even when used jointly with a state-of-the-art projection-data enhancement approach using machine-learning. These results are obtained for 2D and 3D imaging, on large biomedical datasets, in both projection space and image space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge