Data classification using the Dempster-Shafer method
Paper and Code
Sep 02, 2014
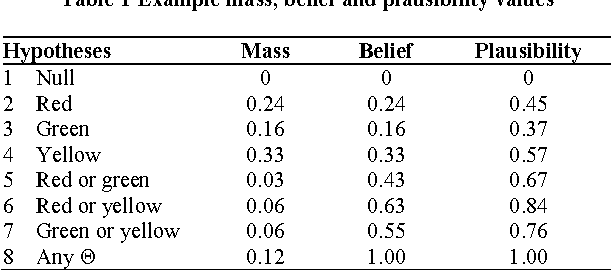
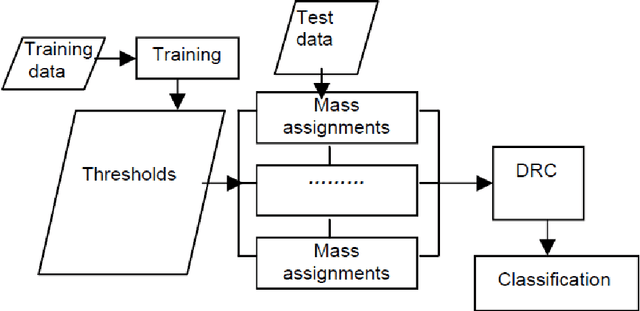

In this paper, the Dempster-Shafer method is employed as the theoretical basis for creating data classification systems. Testing is carried out using three popular (multiple attribute) benchmark datasets that have two, three and four classes. In each case, a subset of the available data is used for training to establish thresholds, limits or likelihoods of class membership for each attribute, and hence create mass functions that establish probability of class membership for each attribute of the test data. Classification of each data item is achieved by combination of these probabilities via Dempster's Rule of Combination. Results for the first two datasets show extremely high classification accuracy that is competitive with other popular methods. The third dataset is non-numerical and difficult to classify, but good results can be achieved provided the system and mass functions are designed carefully and the right attributes are chosen for combination. In all cases the Dempster-Shafer method provides comparable performance to other more popular algorithms, but the overhead of generating accurate mass functions increases the complexity with the addition of new attributes. Overall, the results suggest that the D-S approach provides a suitable framework for the design of classification systems and that automating the mass function design and calculation would increase the viability of the algorithm for complex classification problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge