Cyclical Kernel Adaptive Metropolis
Paper and Code
Jun 30, 2022


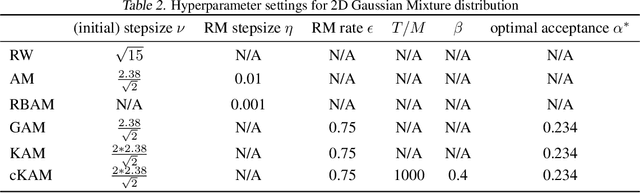
We propose cKAM, cyclical Kernel Adaptive Metropolis, which incorporates a cyclical stepsize scheme to allow control for exploration and sampling. We show that on a crafted bimodal distribution, existing Adaptive Metropolis type algorithms would fail to converge to the true posterior distribution. We point out that this is because adaptive samplers estimates the local/global covariance structure using past history of the chain, which will lead to adaptive algorithms be trapped in a local mode. We demonstrate that cKAM encourages exploration of the posterior distribution and allows the sampler to escape from a local mode, while maintaining the high performance of adaptive methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge