Cubic Spline Smoothing Compensation for Irregularly Sampled Sequences
Paper and Code
Oct 03, 2020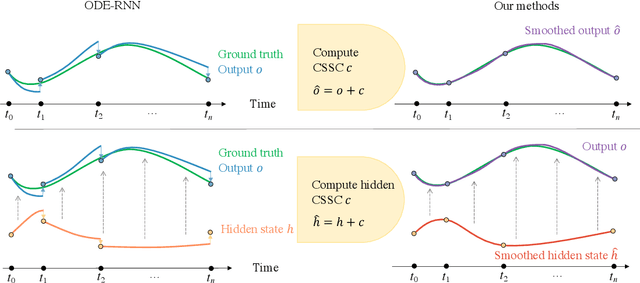

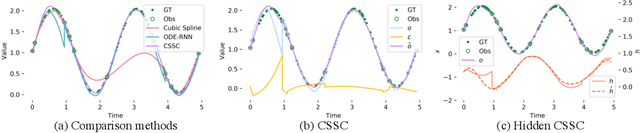
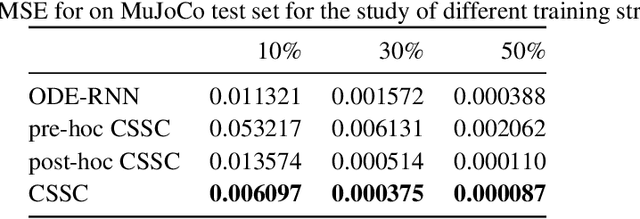
The marriage of recurrent neural networks and neural ordinary differential networks (ODE-RNN) is effective in modeling irregularly-observed sequences. While ODE produces the smooth hidden states between observation intervals, the RNN will trigger a hidden state jump when a new observation arrives, thus cause the interpolation discontinuity problem. To address this issue, we propose the cubic spline smoothing compensation, which is a stand-alone module upon either the output or the hidden state of ODE-RNN and can be trained end-to-end. We derive its analytical solution and provide its theoretical interpolation error bound. Extensive experiments indicate its merits over both ODE-RNN and cubic spline interpolation.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge