Counterexample-guided Planning
Paper and Code
Jul 04, 2012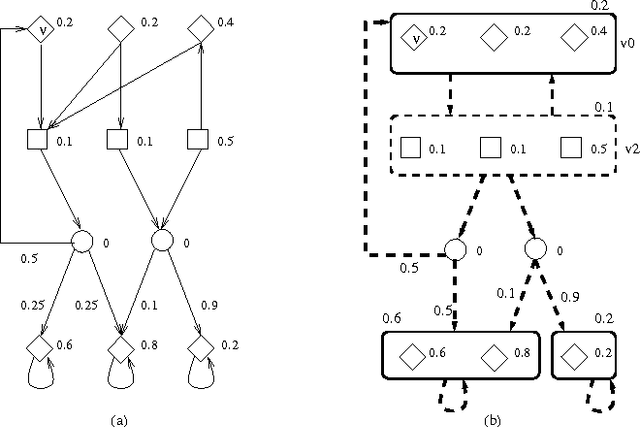
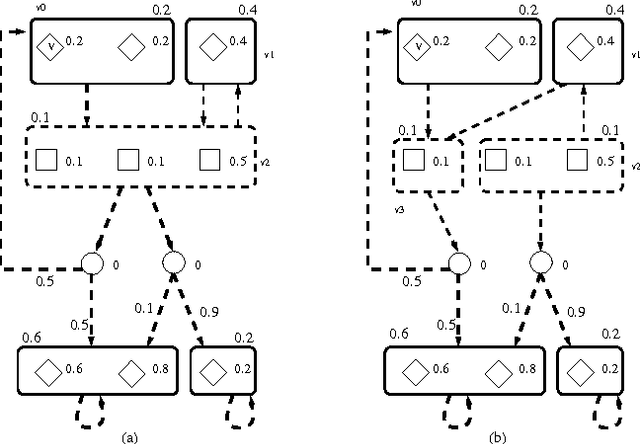
Planning in adversarial and uncertain environments can be modeled as the problem of devising strategies in stochastic perfect information games. These games are generalizations of Markov decision processes (MDPs): there are two (adversarial) players, and a source of randomness. The main practical obstacle to computing winning strategies in such games is the size of the state space. In practice therefore, one typically works with abstractions of the model. The diffculty is to come up with an abstraction that is neither too coarse to remove all winning strategies (plans), nor too fine to be intractable. In verification, the paradigm of counterexample-guided abstraction refinement has been successful to construct useful but parsimonious abstractions automatically. We extend this paradigm to probabilistic models (namely, perfect information games and, as a special case, MDPs). This allows us to apply the counterexample-guided abstraction paradigm to the AI planning problem. As special cases, we get planning algorithms for MDPs and deterministic systems that automatically construct system abstractions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge