Cost-Efficient Deployment of a Reliable Multi-UAV Unmanned Aerial System
Paper and Code
Aug 30, 2022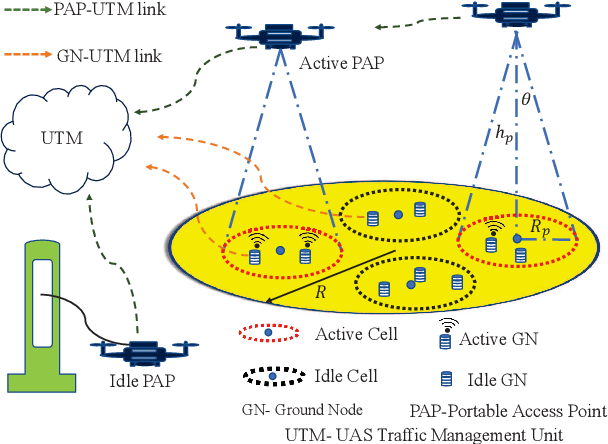
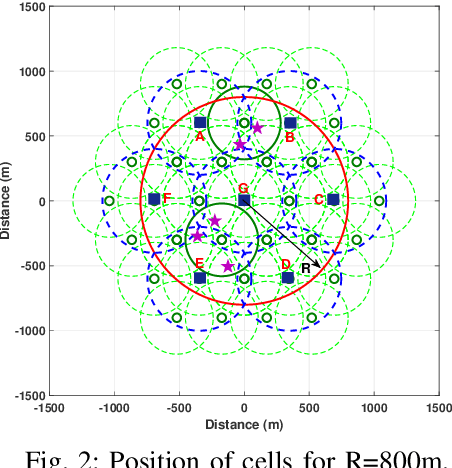
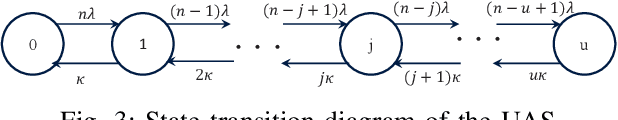
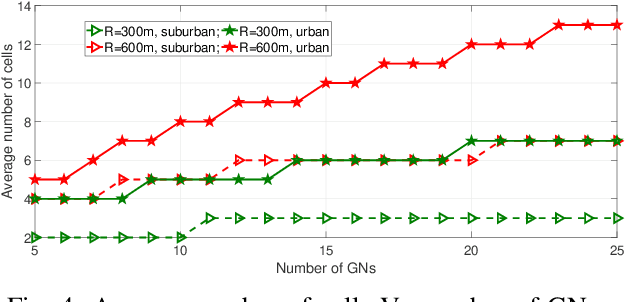
In this work, we study the trade-off between the reliability and the investment cost of an unmanned aerial system (UAS) consisting of a set of unmanned aerial vehicles (UAVs) carrying radio access nodes, called portable access points (PAPs)), deployed to serve a set of ground nodes (GNs). Using the proposed algorithm, a given geographical region is equivalently represented as a set of circular regions, where each circle represents the coverage region of a PAP. Then, the steady-state availability of the UAS is analytically derived by modelling it as a continuous time birth-death Markov decision process (MDP). Numerical evaluations show that the investment cost to guarantee a given steady-state availability to a set of GNs can be reduced by considering the traffic demand and distribution of GNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge