Correlated Variational Auto-Encoders
Paper and Code
May 16, 2019
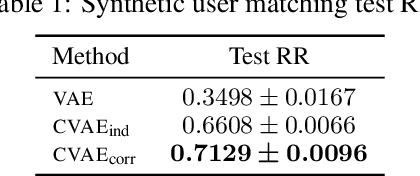

Variational Auto-Encoders (VAEs) are capable of learning latent representations for high dimensional data. However, due to the i.i.d. assumption, VAEs only optimize the singleton variational distributions and fail to account for the correlations between data points, which might be crucial for learning latent representations from dataset where a priori we know correlations exist. We propose Correlated Variational Auto-Encoders (CVAEs) that can take the correlation structure into consideration when learning latent representations with VAEs. CVAEs apply a prior based on the correlation structure. To address the intractability introduced by the correlated prior, we develop an approximation by average of a set of tractable lower bounds over all maximal acyclic subgraphs of the undirected correlation graph. Experimental results on matching and link prediction on public benchmark rating datasets and spectral clustering on a synthetic dataset show the effectiveness of the proposed method over baseline algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge