Cooperative-Competitive Reinforcement Learning with History-Dependent Rewards
Paper and Code
Oct 15, 2020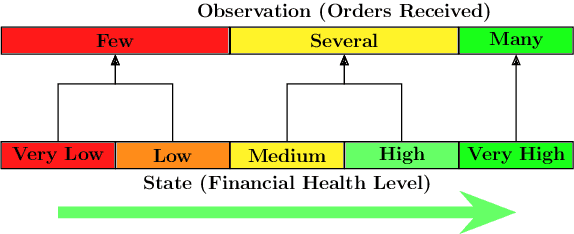

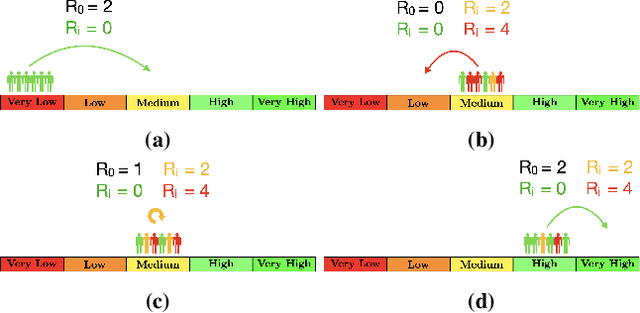
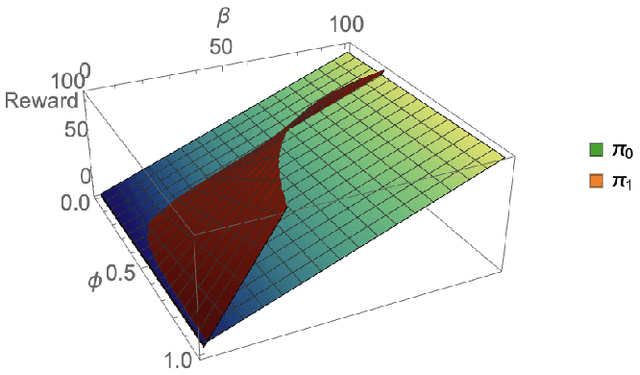
Consider a typical organization whose worker agents seek to collectively cooperate for its general betterment. However, each individual agent simultaneously seeks to act to secure a larger chunk than its co-workers of the annual increment in compensation, which usually comes from a {\em fixed} pot. As such, the individual agent in the organization must cooperate and compete. Another feature of many organizations is that a worker receives a bonus, which is often a fraction of previous year's total profit. As such, the agent derives a reward that is also partly dependent on historical performance. How should the individual agent decide to act in this context? Few methods for the mixed cooperative-competitive setting have been presented in recent years, but these are challenged by problem domains whose reward functions do not depend on the current state and action only. Recent deep multi-agent reinforcement learning (MARL) methods using long short-term memory (LSTM) may be used, but these adopt a joint perspective to the interaction or require explicit exchange of information among the agents to promote cooperation, which may not be possible under competition. In this paper, we first show that the agent's decision-making problem can be modeled as an interactive partially observable Markov decision process (I-POMDP) that captures the dynamic of a history-dependent reward. We present an interactive advantage actor-critic method (IA2C$^+$), which combines the independent advantage actor-critic network with a belief filter that maintains a belief distribution over other agents' models. Empirical results show that IA2C$^+$ learns the optimal policy faster and more robustly than several other baselines including one that uses a LSTM, even when attributed models are incorrect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge